Uji Korelasi Pearson merupakan metode statistik yang ampuh untuk mengungkap hubungan antara dua variabel numerik. Bayangkan Anda ingin meneliti apakah ada korelasi antara jam belajar dan nilai ujian mahasiswa. Uji ini akan membantu menjawab pertanyaan tersebut, menunjukkan seberapa kuat dan arah hubungan antara kedua variabel tersebut. Dengan memahami konsep dasar, asumsi, dan interpretasi hasil uji korelasi Pearson, kita dapat menganalisis data dengan lebih akurat dan mengambil kesimpulan yang bermakna.
Artikel ini akan membahas secara lengkap tahapan dalam melakukan uji korelasi Pearson, mulai dari pemahaman konsep dasar hingga interpretasi hasil. Kita akan mempelajari berbagai jenis korelasi, asumsi yang perlu dipenuhi, langkah-langkah perhitungan baik manual maupun menggunakan software statistik, serta kekuatan dan keterbatasan metode ini. Dengan demikian, diharapkan pembaca dapat mengaplikasikan uji korelasi Pearson dengan tepat dan percaya diri dalam menganalisis data penelitian.
Pengantar Uji Korelasi Pearson

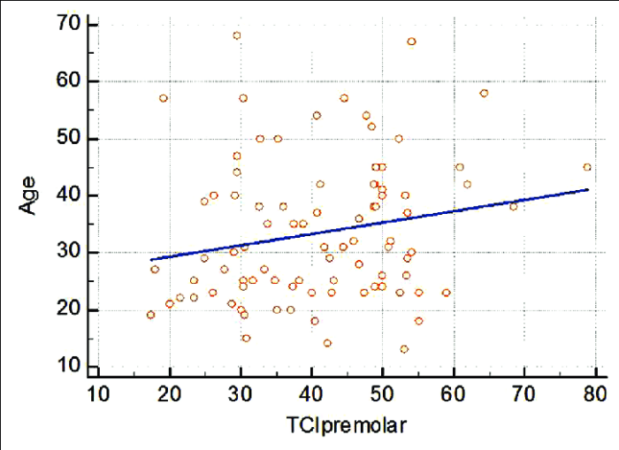
Uji korelasi Pearson merupakan metode statistik yang digunakan untuk mengukur kekuatan dan arah hubungan linier antara dua variabel interval atau rasio. Metode ini sangat berguna dalam berbagai bidang penelitian untuk mengidentifikasi keterkaitan antara dua variabel yang diukur secara kuantitatif. Hasil uji korelasi Pearson dinyatakan dalam koefisien korelasi (r), yang berkisar antara -1 hingga +1.
Dengan memahami konsep korelasi Pearson, peneliti dapat memperoleh pemahaman yang lebih mendalam tentang hubungan antar variabel dalam suatu fenomena. Hal ini memungkinkan peneliti untuk membangun model yang lebih akurat dan membuat prediksi yang lebih baik.
Contoh Kasus Penggunaan Uji Korelasi Pearson
Sebagai contoh, sebuah penelitian ingin menyelidiki hubungan antara jumlah jam belajar (variabel X) dan nilai ujian akhir (variabel Y) mahasiswa. Dengan menggunakan uji korelasi Pearson, peneliti dapat menganalisis apakah terdapat hubungan linier antara kedua variabel tersebut dan seberapa kuat hubungan tersebut. Jika ditemukan korelasi positif yang signifikan, maka dapat disimpulkan bahwa semakin banyak jam belajar, semakin tinggi nilai ujian akhir yang diperoleh.
Contoh lain, dalam bidang kesehatan, korelasi Pearson dapat digunakan untuk mengkaji hubungan antara indeks massa tubuh (BMI) dan tekanan darah. Peneliti dapat menguji hipotesis apakah terdapat hubungan positif antara BMI dan tekanan darah, yang menunjukkan peningkatan tekanan darah seiring peningkatan BMI.
Variabel yang Cocok untuk Analisis Korelasi Pearson
Uji korelasi Pearson paling tepat digunakan untuk menganalisis data yang berskala interval atau rasio. Variabel-variabel tersebut harus memiliki distribusi data yang mendekati normal. Contoh variabel yang cocok antara lain: tinggi badan, berat badan, nilai ujian, pendapatan, suhu, dan sebagainya. Variabel kategorikal atau ordinal tidak cocok untuk dianalisis menggunakan uji korelasi Pearson.
Jenis-jenis Korelasi dan Interpretasinya
Koefisien korelasi (r) yang dihasilkan dari uji korelasi Pearson dapat menunjukkan tiga jenis korelasi, yaitu positif, negatif, dan tidak berkorelasi. Berikut tabel yang merangkum jenis-jenis korelasi beserta interpretasinya:
| Jenis Korelasi | Deskripsi | Interpretasi | Contoh Ilustrasi |
|---|---|---|---|
| Positif | Ketika nilai satu variabel meningkat, nilai variabel lainnya juga cenderung meningkat. | Menunjukkan hubungan searah antara dua variabel. Semakin tinggi nilai r, semakin kuat hubungan positifnya. | Hubungan antara jumlah jam belajar dan nilai ujian. Semakin banyak jam belajar, semakin tinggi nilai ujian yang diperoleh. |
| Negatif | Ketika nilai satu variabel meningkat, nilai variabel lainnya cenderung menurun. | Menunjukkan hubungan terbalik antara dua variabel. Semakin rendah nilai r (mendekati -1), semakin kuat hubungan negatifnya. | Hubungan antara jumlah rokok yang dihisap per hari dan kapasitas paru-paru. Semakin banyak rokok yang dihisap, semakin rendah kapasitas paru-paru. |
| Tidak Berkorelasi | Tidak terdapat hubungan linier antara kedua variabel. | Nilai r mendekati 0. Artinya, perubahan pada satu variabel tidak mempengaruhi perubahan pada variabel lainnya. | Hubungan antara warna mata dan tinggi badan. Tidak ada hubungan linier yang signifikan antara warna mata dan tinggi badan seseorang. |
Asumsi Uji Korelasi Pearson
Uji korelasi Pearson, meskipun umum digunakan, memiliki beberapa asumsi yang harus dipenuhi untuk menghasilkan hasil yang valid dan dapat diinterpretasikan dengan benar. Pengabaian asumsi-asumsi ini dapat menyebabkan kesimpulan yang salah mengenai hubungan antara variabel yang diteliti. Oleh karena itu, penting untuk memahami dan memeriksa asumsi-asumsi ini sebelum melakukan uji korelasi.
Asumsi-Asumsi Uji Korelasi Pearson
Sebelum menjalankan uji korelasi Pearson, ada beberapa asumsi yang perlu dipenuhi. Kegagalan dalam memenuhi asumsi ini dapat memengaruhi keakuratan dan interpretasi hasil uji. Asumsi-asumsi tersebut antara lain: data berdistribusi normal, hubungan antara variabel bersifat linear, dan data berskala interval atau rasio. Penjelasan lebih detail akan diuraikan di bawah ini.
Dampak Pelanggaran Asumsi
Jika asumsi-asumsi uji korelasi Pearson tidak terpenuhi, hasil uji dapat menjadi bias dan tidak akurat. Misalnya, jika data tidak berdistribusi normal, nilai koefisien korelasi yang dihasilkan mungkin tidak mencerminkan hubungan sebenarnya antara variabel. Demikian pula, jika hubungan antara variabel bersifat non-linear, uji korelasi Pearson tidak akan mampu menangkap hubungan tersebut secara tepat. Akibatnya, kesimpulan yang ditarik dari analisis tersebut dapat menyesatkan.
Prosedur Pengecekan Normalitas Data
Untuk memeriksa normalitas data, beberapa metode dapat digunakan. Metode visual seperti histogram dan Q-Q plot dapat memberikan gambaran awal mengenai distribusi data. Jika data terlihat mencengang atau memiliki outlier yang signifikan, maka normalitas data patut dipertanyakan. Selain metode visual, uji statistik seperti uji Kolmogorov-Smirnov atau uji Shapiro-Wilk dapat digunakan untuk menguji secara formal apakah data berdistribusi normal.
Uji Shapiro-Wilk umumnya lebih disukai untuk sampel berukuran kecil. Interpretasi hasil uji ini biasanya didasarkan pada nilai p-value. Jika nilai p-value lebih besar dari tingkat signifikansi yang telah ditentukan (misalnya, 0.05), maka hipotesis nol (data berdistribusi normal) tidak dapat ditolak.
Menangani Data yang Tidak Memenuhi Asumsi
Jika data tidak memenuhi asumsi normalitas, beberapa pendekatan dapat dilakukan. Transformasi data, seperti transformasi logaritma atau akar pangkat dua, dapat membantu menormalkan distribusi data. Alternatif lain adalah menggunakan uji korelasi non-parametrik, seperti uji korelasi Spearman atau Kendall’s tau, yang tidak memerlukan asumsi normalitas. Pilihan metode penanganan bergantung pada jenis pelanggaran asumsi dan karakteristik data. Untuk data dengan outlier yang signifikan, perlu dipertimbangkan untuk melakukan analisis sensitivitas atau menghilangkan outlier tersebut setelah dilakukan pemeriksaan lebih lanjut.
Contoh Kasus Pelanggaran Asumsi dan Solusinya
Misalkan kita ingin menguji korelasi antara pendapatan (dalam jutaan rupiah) dan tingkat kepuasan kerja (skala 1-10). Setelah dilakukan pengujian, ditemukan bahwa data pendapatan tidak berdistribusi normal. Salah satu solusi yang dapat dilakukan adalah dengan melakukan transformasi logaritma pada data pendapatan. Dengan transformasi ini, diharapkan distribusi data pendapatan akan mendekati normal. Jika setelah transformasi data masih tidak memenuhi asumsi normalitas, maka uji korelasi Spearman dapat digunakan sebagai alternatif.
Contoh lain, jika hubungan antara variabel diketahui non-linear, maka penggunaan uji korelasi Pearson tidak tepat dan sebaiknya dipertimbangkan penggunaan model regresi non-linear atau teknik analisis lain yang sesuai.
Prosedur Perhitungan Uji Korelasi Pearson
Uji korelasi Pearson digunakan untuk mengukur kekuatan dan arah hubungan linier antara dua variabel interval atau rasio. Perhitungannya dapat dilakukan secara manual, meskipun untuk data yang besar, penggunaan software statistik lebih efisien. Berikut uraian langkah-langkah perhitungannya.
Perhitungan Manual Uji Korelasi Pearson
Perhitungan manual melibatkan beberapa langkah, mulai dari menghitung rata-rata dan deviasi standar masing-masing variabel hingga menghitung koefisien korelasi. Proses ini membutuhkan ketelitian dan perhitungan yang cermat, terutama untuk dataset yang besar. Berikut langkah-langkahnya:
- Hitung rata-rata (mean) masing-masing variabel (X dan Y).
- Hitung deviasi setiap skor dari rata-rata masing-masing variabel (X – X̄ dan Y – Ȳ).
- Kalikan deviasi setiap skor dari variabel X dengan deviasi skor yang bersesuaian dari variabel Y.
- Jumlahkan hasil perkalian deviasi dari langkah 3.
- Hitung deviasi standar masing-masing variabel (X dan Y).
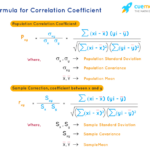
- Hitung koefisien korelasi Pearson (r) menggunakan rumus:
r = Σ[(Xi – X̄)(Yi – Ȳ)] / √[Σ(Xi – X̄)²
Σ(Yi – Ȳ)²]
Contoh Perhitungan dengan Data Numerik Sederhana
Misalkan kita memiliki data tinggi badan (X) dan berat badan (Y) dari lima orang:
| Individu | Tinggi Badan (X) (cm) | Berat Badan (Y) (kg) |
|---|---|---|
| 1 | 160 | 55 |
| 2 | 170 | 65 |
| 3 | 165 | 60 |
| 4 | 175 | 70 |
| 5 | 180 | 75 |
Dengan mengikuti langkah-langkah di atas, kita dapat menghitung koefisien korelasi Pearson. Perhitungan detailnya akan menghasilkan nilai ‘r’ yang menunjukkan kekuatan dan arah hubungan antara tinggi dan berat badan. Nilai ‘r’ berkisar antara -1 hingga +1. Nilai mendekati +1 menunjukkan korelasi positif yang kuat, mendekati -1 menunjukkan korelasi negatif yang kuat, dan mendekati 0 menunjukkan tidak ada korelasi.
Perhitungan Uji Korelasi Pearson Menggunakan Software Statistik
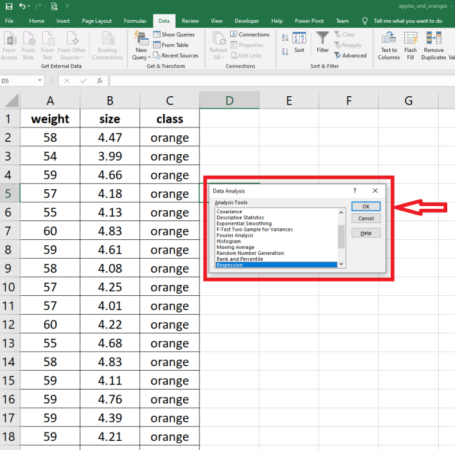
Software statistik seperti SPSS, R, atau Python (dengan library seperti SciPy) memudahkan perhitungan uji korelasi Pearson, terutama untuk dataset yang besar dan kompleks. Prosesnya umumnya melibatkan memasukkan data, memilih prosedur uji korelasi Pearson, dan kemudian software akan menghitung koefisien korelasi beserta nilai signifikansi (p-value).
Sebagai contoh, di SPSS, langkah umum meliputi: import data, pilih menu Analyze > Correlate > Bivariate, masukkan variabel yang akan diuji ke kotak Variables, dan klik OK. Software akan menampilkan hasil perhitungan, termasuk nilai r dan p-value. Interpretasi hasil mengikuti prinsip yang sama seperti perhitungan manual.
Interpretasi Hasil Uji Korelasi Pearson
Setelah melakukan uji korelasi Pearson, langkah selanjutnya adalah menginterpretasi hasil yang diperoleh. Interpretasi ini meliputi pemahaman nilai koefisien korelasi (r) dan nilai p-value. Kedua nilai ini memberikan gambaran yang komprehensif tentang kekuatan dan signifikansi hubungan antara dua variabel yang diteliti.
Nilai Koefisien Korelasi (r)
Nilai koefisien korelasi (r) menunjukkan kekuatan dan arah hubungan antara dua variabel. Nilai r berkisar antara -1 hingga +1. Nilai r mendekati +1 menunjukkan korelasi positif yang kuat, artinya ketika satu variabel meningkat, variabel lainnya juga cenderung meningkat. Nilai r mendekati -1 menunjukkan korelasi negatif yang kuat, di mana ketika satu variabel meningkat, variabel lainnya cenderung menurun.
Nilai r mendekati 0 menunjukkan tidak ada korelasi atau korelasi yang sangat lemah antara kedua variabel.
Nilai p-value
Nilai p-value menunjukkan probabilitas mendapatkan hasil uji korelasi yang sekurang-kurangnya se-ekstrim hasil yang diamati, dengan asumsi tidak ada korelasi antara kedua variabel. Nilai p-value yang kecil (biasanya kurang dari 0.05) menunjukkan bahwa hubungan antara kedua variabel signifikan secara statistik, artinya kecil kemungkinan hasil tersebut terjadi secara kebetulan. Semakin kecil nilai p-value, semakin kuat bukti bahwa terdapat hubungan yang nyata antara kedua variabel.
Contoh Interpretasi Hasil Uji Korelasi Pearson
Berikut beberapa contoh interpretasi dengan nilai r dan p-value yang berbeda:
- Contoh 1: r = 0.8, p-value = 0.
01. Interpretasi: Terdapat korelasi positif yang kuat dan signifikan secara statistik antara kedua variabel. Kemungkinan besar peningkatan pada satu variabel diiringi peningkatan pada variabel lainnya. - Contoh 2: r = -0.3, p-value = 0.
08. Interpretasi: Terdapat korelasi negatif yang lemah, dan tidak signifikan secara statistik antara kedua variabel. Hubungan antara kedua variabel ini mungkin terjadi secara kebetulan. - Contoh 3: r = 0.2, p-value = 0.
03. Interpretasi: Terdapat korelasi positif yang lemah, namun signifikan secara statistik antara kedua variabel. Meskipun kekuatan hubungannya rendah, hasil ini menunjukkan bahwa terdapat hubungan yang nyata, bukan karena kebetulan.
Perbedaan Interpretasi antara Korelasi yang Signifikan dan Tidak Signifikan, Uji korelasi pearson
Perbedaan utama terletak pada kesimpulan yang dapat diambil. Korelasi yang signifikan secara statistik menunjukkan bukti yang cukup kuat untuk menyimpulkan adanya hubungan antara kedua variabel. Sedangkan korelasi yang tidak signifikan secara statistik menunjukkan bahwa tidak ada cukup bukti untuk menolak hipotesis nol (tidak ada korelasi), meskipun mungkin masih ada hubungan yang sebenarnya, namun tidak cukup kuat untuk dibuktikan dengan data yang ada.
Pedoman Umum Interpretasi Hasil Uji Korelasi Pearson: Perhatikan baik nilai koefisien korelasi (r) dan nilai p-value secara bersamaan. Nilai r menunjukkan kekuatan dan arah hubungan, sementara nilai p-value menunjukkan signifikansi statistik hubungan tersebut. Jangan hanya berfokus pada signifikansi statistik saja, perhatikan juga besarnya nilai r untuk memahami kekuatan hubungan yang sebenarnya. Ingatlah bahwa korelasi tidak selalu berarti kausalitas.
Kekuatan dan Keterbatasan Uji Korelasi Pearson
Uji korelasi Pearson, meskipun populer dan bermanfaat, memiliki kekuatan dan keterbatasan yang perlu dipahami sebelum diterapkan. Pemahaman yang baik tentang hal ini akan membantu peneliti memilih metode analisis yang tepat dan menginterpretasikan hasilnya secara akurat. Penting untuk diingat bahwa uji ini hanya mengukur hubungan linier, dan tidak menjelaskan sebab-akibat.
Kekuatan Uji Korelasi Pearson
Uji korelasi Pearson memiliki beberapa kekuatan utama. Ia merupakan metode yang relatif sederhana untuk dihitung dan dipahami, bahkan dengan bantuan perangkat lunak statistik. Hasilnya mudah diinterpretasikan melalui koefisien korelasi (r) yang berkisar antara -1 hingga +1, dimana angka mendekati -1 menunjukkan korelasi negatif yang kuat, angka mendekati +1 menunjukkan korelasi positif yang kuat, dan angka mendekati 0 menunjukkan tidak adanya korelasi linier.
Selain itu, uji ini cukup robust terhadap pelanggaran asumsi normalitas data, terutama jika ukuran sampel cukup besar. Penggunaan uji ini telah teruji dan banyak digunakan dalam berbagai bidang penelitian, sehingga interpretasinya sudah cukup standar dan mudah dibandingkan antar studi.
Keterbatasan Uji Korelasi Pearson
Meskipun memiliki kekuatan, uji korelasi Pearson memiliki beberapa keterbatasan. Yang paling utama adalah asumsi data harus berdistribusi normal. Meskipun relatif robust terhadap pelanggaran asumsi ini, data yang sangat menyimpang dari distribusi normal dapat memengaruhi hasil. Selain itu, uji ini hanya mengukur hubungan linier. Hubungan non-linier, seperti hubungan kuadratik atau eksponensial, tidak akan terdeteksi dengan baik oleh uji ini.
Terakhir, korelasi tidak sama dengan kausalitas. Meskipun terdapat korelasi yang kuat antara dua variabel, hal tersebut tidak secara otomatis membuktikan bahwa satu variabel menyebabkan perubahan pada variabel lainnya. Faktor lain yang tidak terukur dapat berperan sebagai variabel penengah atau konfounding.
Situasi di Mana Uji Korelasi Pearson Kurang Tepat Digunakan
Uji korelasi Pearson kurang tepat digunakan ketika data tidak memenuhi asumsi-asumsinya. Contohnya, ketika data mengandung outlier yang ekstrem, atau ketika hubungan antara variabel bersifat non-linier. Data ordinal atau nominal juga tidak sesuai untuk uji ini. Dalam kasus data yang tidak berdistribusi normal dan ukuran sampel kecil, uji korelasi non-parametrik seperti Spearman atau Kendall mungkin lebih tepat. Begitu pula, jika hubungan antar variabel diduga non-linier, maka perlu dipertimbangkan metode analisis regresi non-linier.
Alternatif Metode Analisis Jika Uji Korelasi Pearson Tidak Sesuai
Beberapa alternatif metode analisis yang dapat digunakan jika uji korelasi Pearson tidak sesuai meliputi uji korelasi Spearman atau Kendall (untuk data ordinal atau data numerik yang tidak memenuhi asumsi normalitas), dan regresi non-linier (untuk hubungan non-linier). Pemilihan metode alternatif bergantung pada jenis data dan bentuk hubungan antara variabel yang diteliti. Misalnya, jika data berupa peringkat (ordinal), uji korelasi Spearman lebih tepat.
Jika hubungan antara variabel terlihat berbentuk kurva, maka regresi non-linier lebih sesuai.
Contoh Kasus di Mana Uji Korelasi Pearson Kurang Tepat dan Metode Alternatif yang Lebih Baik
Misalnya, peneliti ingin menguji hubungan antara tingkat kepuasan kerja (diukur dengan skala Likert, sehingga bersifat ordinal) dan produktivitas karyawan. Karena data tingkat kepuasan kerja bersifat ordinal, maka uji korelasi Pearson kurang tepat. Uji korelasi Spearman akan menjadi alternatif yang lebih baik dalam kasus ini. Contoh lain, jika peneliti ingin menguji hubungan antara dosis obat (variabel independen) dan penurunan tekanan darah (variabel dependen), dan diduga hubungannya bersifat non-linier (misalnya, penurunan tekanan darah meningkat tajam pada dosis rendah, lalu meningkat lebih lambat pada dosis tinggi), maka regresi non-linier, seperti regresi polinomial, lebih tepat daripada korelasi Pearson.
Simpulan Akhir
Uji korelasi Pearson terbukti menjadi alat yang berharga dalam mengungkap hubungan antara variabel numerik. Pemahaman yang mendalam tentang konsep dasar, asumsi, perhitungan, dan interpretasi hasil sangat penting untuk memastikan penggunaan metode ini secara tepat dan efektif. Meskipun memiliki keterbatasan, uji korelasi Pearson tetap menjadi metode analisis yang relevan dan banyak digunakan dalam berbagai bidang penelitian, asalkan asumsinya terpenuhi dan interpretasinya dilakukan secara hati-hati.
Dengan memahami kekuatan dan kelemahannya, peneliti dapat memilih metode analisis yang paling sesuai dengan data dan tujuan penelitian.