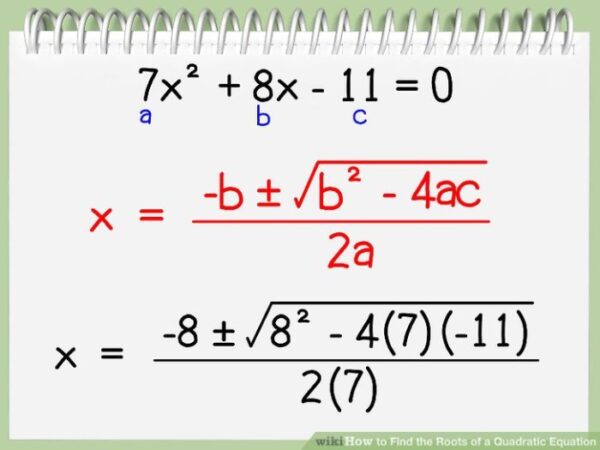Persamaan kuadrat yang akar akarnya 2 dan 3 adalah – Persamaan kuadrat yang akar-akarnya 2 dan 3 adalah topik yang mendasar dalam aljabar. Memahami bagaimana membentuk persamaan kuadrat dari akar-akarnya merupakan kunci untuk menyelesaikan berbagai permasalahan matematika, khususnya yang berkaitan dengan fungsi kuadrat dan grafik parabola. Dengan mengetahui akar-akar, kita dapat membangun persamaan dan menganalisis sifat-sifatnya, seperti titik potong sumbu x, dan bentuk parabola.
Proses pembentukan persamaan kuadrat dari akar-akarnya melibatkan pemahaman tentang faktorisasi dan rumus umum persamaan kuadrat. Kita akan mempelajari bagaimana menggunakan rumus (x – a)(x – b) = 0, di mana ‘a’ dan ‘b’ adalah akar-akar persamaan, untuk mendapatkan bentuk umum persamaan kuadrat. Selanjutnya, kita akan menganalisis hubungan antara koefisien persamaan kuadrat (a, b, dan c) dengan akar-akarnya, dan bagaimana hubungan ini dapat digunakan untuk menyelesaikan berbagai soal, termasuk soal cerita.
Persamaan Kuadrat dari Akar-akar 2 dan 3
Menentukan persamaan kuadrat jika akar-akarnya diketahui merupakan konsep dasar dalam aljabar. Pemahaman tentang hal ini sangat penting untuk menyelesaikan berbagai permasalahan matematika, khususnya yang berkaitan dengan fungsi kuadrat dan grafik parabola.
Bentuk Umum Persamaan Kuadrat
Persamaan kuadrat memiliki bentuk umum ax² + bx + c = 0, di mana a, b, dan c adalah konstanta dan a ≠ 0. Koefisien a, b, dan c menentukan bentuk dan posisi parabola yang diwakilinya. Nilai a menentukan apakah parabola terbuka ke atas (a > 0) atau ke bawah (a < 0), sementara b dan c memengaruhi titik puncak dan titik potong sumbu y.
Persamaan Kuadrat dengan Akar-akar 2 dan 3
Jika akar-akar persamaan kuadrat adalah 2 dan 3, kita dapat menggunakan rumus faktor untuk membentuk persamaan tersebut. Rumus faktor menyatakan bahwa jika α dan β adalah akar-akar persamaan kuadrat, maka persamaan tersebut dapat ditulis sebagai (x – α)(x – β) = 0.
(x – 2)(x – 3) = 0
Dengan demikian, persamaan kuadrat yang akar-akarnya 2 dan 3 adalah (x – 2)(x – 3) = 0.
Penjabaran Persamaan Kuadrat
Untuk mendapatkan bentuk umum persamaan kuadrat, kita perlu menjabarkan persamaan (x – 2)(x – 3) =
0. Dengan menggunakan metode perkalian distributif (FOIL), kita peroleh:
x²
3x – 2x + 6 = 0
Setelah disederhanakan, persamaan kuadratnya menjadi:
x² – 5x + 6 = 0
Ini adalah persamaan kuadrat dengan akar-akar 2 dan 3 dalam bentuk umum ax² + bx + c = 0, di mana a = 1, b = -5, dan c = 6.
Contoh Soal Mencari Persamaan Kuadrat
Sebuah bola dilempar vertikal ke atas. Tinggi bola (h) dalam meter setelah t detik dinyatakan dengan persamaan kuadrat h = -5t² + 20t. Tentukan waktu (t) ketika bola mencapai ketinggian 15 meter. Kita perlu mencari akar-akar persamaan kuadrat -5t² + 20t -15 = 0. Dengan memfaktorkan persamaan tersebut, kita peroleh -5(t-1)(t-3)=0, sehingga akar-akarnya adalah t = 1 dan t = 3 detik.
Ini berarti bola mencapai ketinggian 15 meter pada detik ke-1 dan detik ke-3.
Langkah-langkah Menentukan Persamaan Kuadrat dari Akar-akarnya
- Tentukan akar-akar persamaan kuadrat (misalnya, α dan β).
- Buatlah persamaan faktor (x – α)(x – β) = 0.
- Jabarkan persamaan faktor tersebut menggunakan metode perkalian distributif (FOIL).
- Sederhanakan persamaan yang telah dijabarkan untuk mendapatkan bentuk umum persamaan kuadrat ax² + bx + c = 0.
Menentukan Nilai Koefisien Persamaan Kuadrat
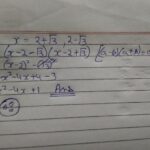
Setelah mengetahui bahwa persamaan kuadrat yang akar-akarnya 2 dan 3 adalah x²
-5x + 6 = 0, langkah selanjutnya adalah memahami koefisien-koefisiennya dan bagaimana pengaruhnya terhadap grafik persamaan tersebut. Pemahaman ini penting karena koefisien menentukan bentuk dan posisi parabola pada bidang koordinat.
Pada persamaan kuadrat umum ax² + bx + c = 0, a, b, dan c mewakili koefisien-koefisiennya. Dalam persamaan x²
-5x + 6 = 0, kita dapat mengidentifikasi a = 1, b = -5, dan c = 6. Koefisien a menentukan arah pembukaan parabola (a > 0 parabola terbuka ke atas, a < 0 parabola terbuka ke bawah), koefisien b memengaruhi posisi sumbu simetri, dan koefisien c menunjukkan titik potong parabola dengan sumbu y.
Pengaruh Perubahan Koefisien terhadap Grafik
Perubahan nilai koefisien akan berdampak signifikan pada bentuk dan posisi parabola. Misalnya, jika kita ubah koefisien a menjadi -1, persamaan menjadi -x²
-5x + 6 = 0. Parabola akan terbalik, membuka ke bawah. Perubahan pada b akan menggeser sumbu simetri parabola, sementara perubahan pada c akan menggeser parabola secara vertikal ke atas atau ke bawah. Perubahan pada a, b, dan c secara bersamaan akan menghasilkan kombinasi dari efek-efek tersebut.
Ilustrasi Grafik Persamaan Kuadrat
Bayangkan sebuah parabola yang terbuka ke atas (karena a = 1 > 0) dengan titik puncak berada di titik (2.5, -0.25). Parabola ini memotong sumbu x di titik (2, 0) dan (3, 0), yang sesuai dengan akar-akar persamaan. Titik potong sumbu y adalah (0, 6), sesuai dengan nilai c. Jika a berubah menjadi -1, parabola akan terbalik, membuka ke bawah, dengan titik puncak tetap berada di (2.5, 0.25) namun parabola sekarang akan memotong sumbu y di (0,6) dan memantul di sumbu x di (2,0) dan (3,0).
Tabel Perbandingan Persamaan Kuadrat
Berikut tabel perbandingan beberapa persamaan kuadrat dengan nilai koefisien a, b, dan c yang berbeda. Perlu diingat bahwa ini hanya beberapa contoh, dan variasi yang mungkin sangat banyak.
| Persamaan Kuadrat | a | b | c | Deskripsi Grafik |
|---|---|---|---|---|
| x² – 5x + 6 = 0 | 1 | -5 | 6 | Parabola terbuka ke atas, titik puncak di (2.5, -0.25), memotong sumbu x di (2,0) dan (3,0), memotong sumbu y di (0,6). |
| -x² – 5x + 6 = 0 | -1 | -5 | 6 | Parabola terbuka ke bawah, titik puncak di (2.5, 0.25), memotong sumbu x di (2,0) dan (3,0), memotong sumbu y di (0,6). |
| x² + x – 6 = 0 | 1 | 1 | -6 | Parabola terbuka ke atas, memotong sumbu x di (-3,0) dan (2,0), memotong sumbu y di (0,-6). |
| 2x² – 8x + 6 = 0 | 2 | -8 | 6 | Parabola terbuka ke atas, lebih sempit daripada x²
|
Hubungan antara Akar-akar dan Koefisien
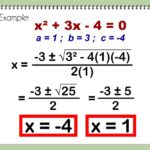
Setelah kita menemukan akar-akar persamaan kuadrat, yaitu 2 dan 3, kita dapat menyelidiki hubungan yang menarik antara akar-akar ini dengan koefisien persamaan kuadratnya. Hubungan ini memberikan cara alternatif untuk memverifikasi solusi dan bahkan untuk membangun persamaan kuadrat baru.
Jumlah Akar-akar dan Koefisien b/a
Pada persamaan kuadrat umum ax² + bx + c = 0, terdapat hubungan sederhana antara jumlah akar-akar (misal α dan β) dan koefisien-koefisiennya. Jumlah akar-akar (α + β) selalu sama dengan -b/a. Dalam kasus kita, dengan akar-akar 2 dan 3, jumlahnya adalah 2 + 3 = 5. Mari kita asumsikan persamaan kuadrat kita adalah x²
-5x + 6 = 0 (kita akan melihat bagaimana mendapatkan persamaan ini nanti).
Di sini, a = 1, b = -5, dan c = 6. Maka -b/a = -(-5)/1 = 5, yang sama dengan jumlah akar-akar kita.
Hasil Kali Akar-akar dan Koefisien c/a
Selain jumlah akar-akar, hasil kali akar-akar (αβ) juga berhubungan dengan koefisien persamaan kuadrat. Hasil kali akar-akar selalu sama dengan c/a. Untuk akar-akar 2 dan 3, hasil kalinya adalah 2 x 3 = 6. Dengan persamaan x²
-5x + 6 = 0, kita punya c/a = 6/1 = 6, yang sesuai dengan hasil kali akar-akar.
Verifikasi Akar-akar Persamaan Kuadrat, Persamaan kuadrat yang akar akarnya 2 dan 3 adalah
Dengan menggunakan hubungan antara akar-akar dan koefisien, kita dapat memverifikasi apakah akar-akar yang kita temukan benar. Jika jumlah dan hasil kali akar-akar sesuai dengan -b/a dan c/a, maka akar-akar tersebut valid. Dalam contoh kita, jumlah akar-akar (5) sama dengan -b/a (5), dan hasil kali akar-akar (6) sama dengan c/a (6). Ini mengkonfirmasi bahwa 2 dan 3 memang akar-akar dari persamaan kuadrat yang kita gunakan.
Menentukan Persamaan Kuadrat dari Akar-akarnya
Kita dapat menggunakan hubungan akar-akar dan koefisien untuk membangun persamaan kuadrat tanpa perlu menggunakan rumus (x – α)(x – β) = 0. Jika kita tahu akar-akarnya adalah 2 dan 3, kita tahu bahwa jumlah akar-akar adalah 5 dan hasil kalinya adalah 6. Dengan demikian, kita dapat langsung membangun persamaan kuadratnya sebagai x²
-(jumlah akar-akar)x + (hasil kali akar-akar) = 0, atau x²
-5x + 6 = 0.
Memahami hubungan antara akar-akar dan koefisien persamaan kuadrat sangat penting karena memberikan cara efisien untuk memverifikasi solusi, membangun persamaan kuadrat baru, dan menyelesaikan berbagai masalah terkait persamaan kuadrat dengan lebih cepat dan mudah. Kemampuan ini sangat berguna dalam berbagai aplikasi matematika dan ilmu terapan.
Penerapan dalam Soal Certa
Persamaan kuadrat, dengan akar-akarnya yang telah diketahui, memiliki penerapan yang luas dalam menyelesaikan berbagai masalah kontekstual atau soal cerita. Kemampuan untuk membangun persamaan kuadrat dari akar-akarnya merupakan kunci untuk memodelkan situasi nyata ke dalam bentuk matematis yang dapat dipecahkan.
Pemahaman ini memungkinkan kita untuk menerjemahkan deskripsi suatu masalah ke dalam persamaan kuadrat, kemudian menemukan solusi yang relevan dengan konteks masalah tersebut. Berikut ini beberapa contoh penerapannya dalam soal cerita.
Soal Cerita dan Penyelesaiannya
Sebuah taman berbentuk persegi panjang memiliki luas 6 m 2. Panjang taman tersebut 1 meter lebih panjang dari lebarnya. Tentukan panjang dan lebar taman tersebut.
Misalkan lebar taman adalah x meter. Maka panjang taman adalah x + 1 meter. Luas taman adalah hasil kali panjang dan lebar, sehingga kita peroleh persamaan:
x(x + 1) = 6
Persamaan ini dapat disederhanakan menjadi:
x2 + x – 6 = 0
Persamaan kuadrat ini memiliki akar-akar 2 dan -3. Karena lebar taman tidak mungkin negatif, maka lebar taman adalah 2 meter. Dengan demikian, panjang taman adalah 2 + 1 = 3 meter.
Contoh Soal Cerita Lain
Sebuah roket diluncurkan vertikal ke atas. Tinggi roket (dalam meter) setelah t detik diberikan oleh persamaan h(t) = -5t2 + 20t + 25 . Tentukan waktu saat roket mencapai ketinggian 0 meter (saat roket menyentuh tanah).
Kita perlu menyelesaikan persamaan kuadrat -5t2 + 20t + 25 = 0 . Setelah disederhanakan menjadi t2
-4t – 5 = 0 , kita dapatkan akar-akarnya adalah 5 dan -1. Karena waktu tidak mungkin negatif, maka roket menyentuh tanah setelah 5 detik.
Berbagai Tipe Soal Cerita yang Melibatkan Persamaan Kuadrat
Konsep persamaan kuadrat dan akar-akarnya dapat diaplikasikan dalam berbagai tipe soal cerita, termasuk masalah geometri (luas, volume, keliling), masalah gerak (kecepatan, percepatan, jarak), masalah keuangan (bunga, investasi), dan masalah optimasi (memaksimalkan keuntungan, meminimalkan biaya).
Variasi soal cerita dapat melibatkan penentuan persamaan kuadrat dari informasi yang diberikan, seperti akar-akarnya, titik puncaknya, atau beberapa titik yang dilalui grafik fungsi kuadrat. Pemahaman yang kuat tentang hubungan antara koefisien persamaan kuadrat dan sifat-sifat akar-akarnya sangat penting untuk menyelesaikan berbagai jenis soal cerita ini.
Langkah-Langkah Umum Penyelesaian Soal Cerita Persamaan Kuadrat
| Langkah | Deskripsi | Contoh | Catatan |
|---|---|---|---|
| 1. Memahami Masalah | Identifikasi variabel dan informasi yang diberikan dalam soal cerita. | Tentukan variabel yang mewakili panjang dan lebar. | Bacalah soal cerita dengan teliti. |
| 2. Membangun Model Matematis | Terjemahkan informasi dalam soal cerita ke dalam persamaan kuadrat. | Buat persamaan yang merepresentasikan luas persegi panjang. | Gunakan rumus atau prinsip yang relevan. |
| 3. Menyelesaikan Persamaan Kuadrat | Selesaikan persamaan kuadrat untuk menemukan akar-akarnya. | Faktorkan atau gunakan rumus kuadrat. | Pilih metode yang paling tepat. |
| 4. Menganalisis Solusi | Interpretasikan akar-akar persamaan kuadrat dalam konteks soal cerita. | Pilih akar yang sesuai dengan konteks masalah (misalnya, lebar tidak mungkin negatif). | Periksa apakah solusi masuk akal. |
Penutupan: Persamaan Kuadrat Yang Akar Akarnya 2 Dan 3 Adalah
Memahami konsep persamaan kuadrat dan hubungan antara akar-akar serta koefisiennya merupakan fondasi penting dalam matematika. Kemampuan untuk menentukan persamaan kuadrat dari akar-akarnya, atau sebaliknya, membuka jalan untuk memecahkan berbagai masalah yang lebih kompleks. Dengan menguasai konsep ini, kita dapat dengan mudah menganalisis grafik parabola, menentukan titik puncak, dan menyelesaikan berbagai soal cerita yang berkaitan dengan fungsi kuadrat.
Penerapannya pun luas, mulai dari fisika hingga ekonomi.