Contoh Soal Statistika: Panduan Lengkap ini akan memandu Anda menjelajahi dunia statistika melalui berbagai jenis soal, mulai dari yang sederhana hingga yang kompleks. Kita akan membahas soal statistika deskriptif dan inferensial, menganalisis data kualitatif dan kuantitatif, serta mempelajari teknik penyelesaian yang efektif. Siap mengasah kemampuan statistika Anda?
Dari memahami konsep dasar hingga mengaplikasikannya dalam soal-soal yang menantang, panduan ini akan memberikan pemahaman yang komprehensif tentang berbagai topik statistika. Dengan contoh soal yang terstruktur dan penjelasan langkah demi langkah, Anda akan mampu menguasai berbagai teknik penyelesaian dan meningkatkan kemampuan interpretasi hasil analisis statistika.
Jenis Soal Statistika
Statistika, sebagai ilmu yang berkaitan dengan pengumpulan, analisis, interpretasi, presentasi, dan pengorganisasian data, memiliki berbagai jenis soal yang menguji pemahaman konsep dan kemampuan penerapannya. Soal-soal ini dapat dikategorikan berdasarkan pendekatan analisis yang digunakan, mulai dari yang sederhana hingga yang kompleks.
Secara umum, soal statistika dapat dikelompokkan menjadi soal statistika deskriptif dan inferensial. Perbedaan mendasar terletak pada tujuan analisisnya. Statistika deskriptif fokus pada penyajian data, sedangkan statistika inferensial bertujuan untuk menarik kesimpulan dari sampel terhadap populasi.
Perbedaan Soal Statistika Deskriptif dan Inferensial
Statistika deskriptif berfokus pada penyajian data mentah menjadi informasi yang lebih mudah dipahami. Ini meliputi perhitungan rata-rata, median, modus, standar deviasi, dan pembuatan grafik seperti histogram atau diagram batang. Sementara itu, statistika inferensial menggunakan data sampel untuk membuat kesimpulan atau prediksi tentang populasi yang lebih besar. Ini melibatkan uji hipotesis, interval kepercayaan, dan regresi.
Contoh soal statistika deskriptif: Hitunglah rata-rata nilai ujian matematika dari 10 siswa: 70, 80, 90, 75, 85, 95, 78, 88, 92,
82. Sedangkan contoh soal statistika inferensial: Berdasarkan sampel 100 responden, ujilah hipotesis bahwa rata-rata tinggi badan mahasiswa di universitas tertentu adalah 170 cm.
Contoh Soal Statistika dengan Data Kualitatif
Data kualitatif, berupa data kategorikal atau deskriptif, juga dapat dianalisis secara statistik. Contohnya, survei kepuasan pelanggan yang menghasilkan data berupa kategori “Sangat Puas”, “Puas”, “Netral”, “Tidak Puas”, dan “Sangat Tidak Puas”. Analisis data ini dapat menggunakan diagram lingkaran atau tabel frekuensi untuk menggambarkan proporsi setiap kategori.
Contoh soal: Sebuah restoran melakukan survei kepuasan pelanggan. Dari 100 responden, 30 menjawab “Sangat Puas”, 40 menjawab “Puas”, 20 menjawab “Netral”, 5 menjawab “Tidak Puas”, dan 5 menjawab “Sangat Tidak Puas”. Buatlah diagram lingkaran yang menggambarkan proporsi setiap kategori kepuasan pelanggan.
Tabel Perbandingan Jenis Soal Statistika
| Jenis Soal | Deskripsi | Contoh Soal Sederhana | Tingkat Kesulitan |
|---|---|---|---|
| Ukuran Pemusatan (Rata-rata, Median, Modus) | Menghitung nilai tengah dari sekumpulan data. | Tentukan rata-rata dari data: 2, 4, 6, 8, 10. | Mudah |
| Ukuran Penyebaran (Jangkauan, Variansi, Standar Deviasi) | Mengukur sebaran data di sekitar nilai tengah. | Hitung standar deviasi dari data: 10, 12, 14, 16, 18. | Sedang |
| Uji Hipotesis (t-test, z-test) | Menguji perbedaan antara dua kelompok data atau membandingkan data dengan nilai tertentu. | Uji apakah ada perbedaan signifikan antara rata-rata tinggi badan pria dan wanita. | Sulit |
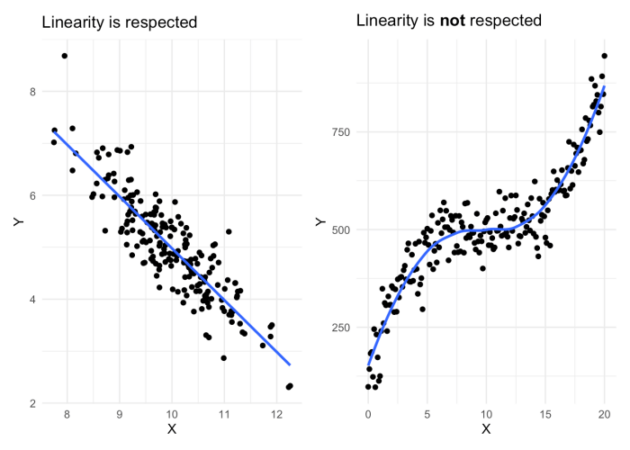
| Regresi Linier | Menentukan hubungan linier antara dua variabel. | Tentukan persamaan regresi linier antara tinggi badan dan berat badan. | Sulit |
Contoh Soal Statistika yang Membutuhkan Penggunaan Software Statistika
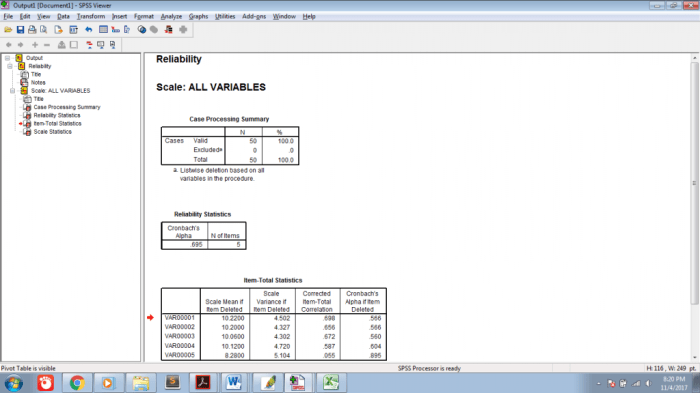
Analisis data yang kompleks, terutama yang melibatkan dataset besar dan uji statistik multivariat, seringkali membutuhkan bantuan software statistika seperti SPSS, R, atau Python dengan library seperti SciPy dan Statsmodels. Contohnya, analisis faktor, analisis klaster, atau analisis jalur memerlukan kemampuan komputasi dan visualisasi data yang disediakan oleh software tersebut.
Contoh soal: Lakukan analisis faktor pada data kepuasan pelanggan yang terdiri dari 20 variabel untuk mengidentifikasi faktor-faktor utama yang mempengaruhi kepuasan pelanggan. Visualisasikan hasil analisis faktor tersebut menggunakan software statistika.
Topik yang Sering Muncul dalam Soal Statistika: Contoh Soal Statistika
Statistika dasar mencakup berbagai konsep yang sering diujikan. Memahami konsep-konsep ini secara mendalam sangat penting untuk menyelesaikan soal statistika dengan tepat. Berikut ini lima topik yang sering muncul dalam soal statistika tingkat dasar, beserta uraian konsep, contoh soal, penyelesaian, dan poin-poin penting.
Ukuran Pemusatan Data
Ukuran pemusatan data digunakan untuk menggambarkan nilai tengah dari suatu kumpulan data. Konsep ini membantu kita memahami kecenderungan pusat data. Terdapat beberapa ukuran pemusatan data, yaitu mean, median, dan modus. Mean merupakan rata-rata hitung, median adalah nilai tengah setelah data diurutkan, dan modus adalah nilai yang paling sering muncul.Contoh Soal: Tentukan mean, median, dan modus dari data berikut: 2, 4, 6, 6, 8, 10.Penyelesaian:Mean = (2 + 4 + 6 + 6 + 8 + 10) / 6 = 6Median = (6 + 6) / 2 = 6Modus = 6
- Mean: Rata-rata hitung dari seluruh data.
- Median: Nilai tengah setelah data diurutkan. Jika jumlah data genap, median adalah rata-rata dari dua nilai tengah.
- Modus: Nilai yang paling sering muncul dalam data. Sebuah data bisa memiliki lebih dari satu modus atau tidak memiliki modus sama sekali.
Ukuran Penyebaran Data
Ukuran penyebaran data menunjukkan seberapa tersebar data dari nilai tengahnya. Ukuran penyebaran yang umum digunakan adalah jangkauan (range), variansi, dan deviasi standar. Jangkauan adalah selisih antara nilai terbesar dan terkecil. Variansi dan deviasi standar mengukur seberapa jauh data tersebar dari mean.Contoh Soal: Tentukan jangkauan, variansi, dan deviasi standar dari data berikut: 2, 4, 6, 6, 8, 10.Penyelesaian:Jangkauan = 10 – 2 = 8Untuk menghitung variansi dan deviasi standar, kita perlu menghitung terlebih dahulu mean (rata-rata): Mean =
6. Kemudian hitung selisih kuadrat masing-masing data dengan mean
(2-6)²=16, (4-6)²=4, (6-6)²=0, (6-6)²=0, (8-6)²=4, (10-6)²=16Jumlah selisih kuadrat: 16+4+0+0+4+16 = 40Variansi = 40 / 6 = 6.67Deviasi Standar = √Variansi = √6.67 ≈ 2.58
- Jangkauan: Selisih antara nilai terbesar dan terkecil.
- Variansi: Rata-rata kuadrat dari selisih antara setiap nilai data dengan mean.
- Deviasi Standar: Akar kuadrat dari variansi. Memberikan gambaran yang lebih mudah dipahami tentang penyebaran data dibandingkan variansi.
Probabilitas
Probabilitas merupakan cabang statistika yang mempelajari kemungkinan terjadinya suatu kejadian. Konsep dasar probabilitas mencakup perhitungan peluang kejadian sederhana, kejadian majemuk, dan kejadian saling lepas.Contoh Soal: Dalam sebuah kotak terdapat 5 bola merah dan 3 bola biru. Jika diambil satu bola secara acak, berapa peluang terambil bola merah?Penyelesaian:Peluang terambil bola merah = (Jumlah bola merah) / (Jumlah total bola) = 5 / (5 + 3) = 5/8 = 0.625
- Kejadian: Suatu peristiwa yang mungkin terjadi.
- Peluang: Ukuran kemungkinan terjadinya suatu kejadian, berkisar antara 0 (tidak mungkin terjadi) hingga 1 (pasti terjadi).
- Kejadian Saling Lepas: Dua kejadian yang tidak dapat terjadi secara bersamaan.
Distribusi Frekuensi
Distribusi frekuensi adalah penyajian data dalam bentuk tabel yang menunjukkan frekuensi kemunculan setiap nilai atau rentang nilai data. Distribusi frekuensi membantu kita untuk memahami pola penyebaran data.Contoh Soal: Buatlah distribusi frekuensi dari data nilai ujian berikut: 70, 80, 85, 90, 75, 80, 95, 85, 70, 80.Penyelesaian:
| Nilai | Frekuensi |
|---|---|
| 70 | 2 |
| 75 | 1 |
| 80 | 3 |
| 85 | 2 |
| 90 | 1 |
| 95 | 1 |
- Frekuensi: Jumlah kemunculan suatu nilai atau rentang nilai.
- Tabel Frekuensi: Tabel yang menyajikan data dan frekuensinya.
- Histogram: Representasi grafis dari distribusi frekuensi.
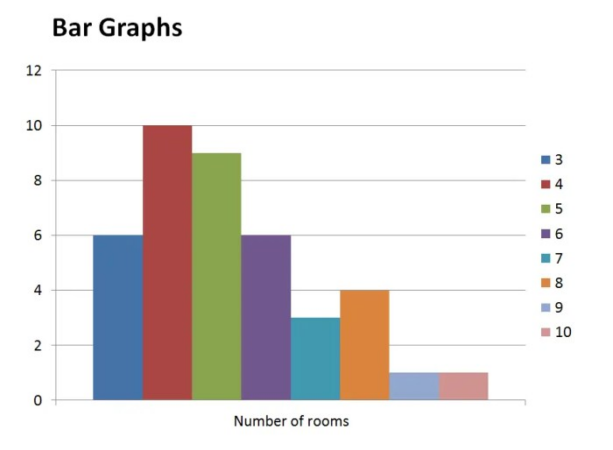
Diagram dan Grafik
Diagram dan grafik digunakan untuk menyajikan data secara visual. Beberapa jenis diagram dan grafik yang umum digunakan adalah histogram, diagram batang, diagram lingkaran, dan poligon frekuensi. Pemahaman tentang cara membaca dan menginterpretasi diagram dan grafik sangat penting.Contoh Soal: Gambarkan diagram batang dari data nilai ujian pada contoh soal distribusi frekuensi di atas.Penyelesaian: (Deskripsi diagram batang: Sumbu X mewakili nilai ujian, sumbu Y mewakili frekuensi.
Setiap nilai ujian diwakili oleh sebuah batang dengan tinggi yang sesuai dengan frekuensinya.)
- Diagram Batang: Menunjukkan perbandingan data kategorik.
- Diagram Lingkaran: Menunjukkan proporsi bagian dari keseluruhan data.
- Histogram: Menunjukkan distribusi frekuensi data numerik.
Teknik Penyelesaian Soal Statistika
Statistika, sebagai ilmu yang mempelajari data, seringkali menghadirkan tantangan tersendiri dalam penyelesaian soal. Pemahaman yang komprehensif tentang konsep dasar dan penerapan metode yang tepat menjadi kunci keberhasilan. Artikel ini akan membahas langkah-langkah umum dalam menyelesaikan soal statistika, disertai contoh dan ilustrasi untuk memperjelas pemahaman.
Langkah-Langkah Umum Penyelesaian Soal Statistika
Secara umum, penyelesaian soal statistika dapat dibagi menjadi beberapa langkah sistematis. Menguasai langkah-langkah ini akan membantu dalam menghadapi berbagai tipe soal, baik yang sederhana maupun kompleks.
- Memahami Soal: Identifikasi jenis soal, data yang diberikan, dan apa yang diminta untuk dihitung atau dianalisis. Pahami setiap istilah dan simbol yang digunakan.
- Memilih Metode yang Tepat: Pilih metode statistika yang sesuai dengan jenis soal dan data yang tersedia. Pertimbangkan distribusi data, tujuan analisis, dan informasi yang dibutuhkan.
- Menghitung dan Menganalisis Data: Lakukan perhitungan yang diperlukan dengan teliti dan akurat. Gunakan kalkulator atau perangkat lunak statistika jika diperlukan. Analisis hasil perhitungan untuk mendapatkan kesimpulan yang valid.
- Menginterpretasikan Hasil: Interpretasikan hasil perhitungan dalam konteks soal. Jelaskan arti dari hasil analisis dan kaitannya dengan pertanyaan yang diajukan.
- Menulis Jawaban: Tulis jawaban secara sistematis dan jelas, sertakan langkah-langkah perhitungan dan interpretasi hasil. Pastikan jawaban mudah dipahami dan sesuai dengan pertanyaan.
Contoh Soal dan Penyelesaiannya
Berikut contoh soal statistika dan langkah-langkah penyelesaiannya:
Soal: Data berat badan (dalam kg) 5 siswa adalah: 45, 50, 48, 52, 47. Hitung rata-rata berat badan siswa tersebut!
- Memahami Soal: Soal meminta kita menghitung rata-rata (mean) dari data berat badan 5 siswa.
- Memilih Metode: Metode yang tepat adalah menghitung rata-rata aritmatika.
- Menghitung dan Menganalisis Data: Rata-rata = (45 + 50 + 48 + 52 + 47) / 5 = 48,4 kg
- Menginterpretasikan Hasil: Rata-rata berat badan 5 siswa tersebut adalah 48,4 kg.
- Menulis Jawaban: Rata-rata berat badan siswa adalah 48,4 kg.
Flowchart Alur Penyelesaian Soal Statistika
Flowchart berikut menggambarkan alur penyelesaian soal statistika secara umum:
[Deskripsi Flowchart: Mulai -> Memahami Soal -> Memilih Metode -> Menghitung Data -> Menganalisis Data -> Menginterpretasikan Hasil -> Menulis Jawaban -> Selesai. Setiap langkah dihubungkan dengan panah.]
Teknik Mengatasi Soal Statistika Kompleks
Soal statistika kompleks seringkali melibatkan lebih dari satu konsep. Beberapa teknik efektif untuk mengatasinya antara lain:
- Memecah Masalah: Pecah masalah kompleks menjadi beberapa bagian yang lebih kecil dan mudah dipahami.
- Menggunakan Diagram: Buat diagram atau grafik untuk memvisualisasikan data dan membantu memahami hubungan antar variabel.
- Mempelajari Konsep Dasar: Kuasai konsep dasar statistika seperti distribusi normal, uji hipotesis, dan regresi.
- Berlatih Terus-Menerus: Kerjakan berbagai soal statistika untuk meningkatkan kemampuan dan pemahaman.
Contoh Soal Statistika yang Melibatkan Lebih dari Satu Konsep
Berikut contoh soal yang membutuhkan pemahaman lebih dari satu konsep statistika:
Soal: Sebuah perusahaan ingin mengetahui apakah ada perbedaan rata-rata penjualan produk A dan produk B. Data penjualan (dalam jutaan rupiah) selama 10 bulan terakhir sebagai berikut: Produk A: 10, 12, 15, 11, 13, 14, 16, 12, 18, 15; Produk B: 8, 9, 11, 10, 12, 13, 9, 11, 14, 10. Gunakan uji t untuk menguji perbedaan rata-rata penjualan kedua produk tersebut dengan tingkat signifikansi 5%.
Penyelesaian soal ini membutuhkan pemahaman tentang perhitungan rata-rata, standar deviasi, dan uji t untuk membandingkan dua rata-rata. Langkah-langkah penyelesaiannya akan melibatkan perhitungan statistik deskriptif (rata-rata dan standar deviasi) untuk kedua produk, kemudian dilanjutkan dengan perhitungan uji t dan interpretasi nilai p-value untuk menentukan apakah terdapat perbedaan signifikan antara rata-rata penjualan kedua produk tersebut.
Sumber Belajar Soal Statistika
Mempelajari statistika membutuhkan latihan soal yang cukup. Keberhasilan dalam memahami konsep statistika sangat bergantung pada pemahaman yang kuat dan kemampuan untuk menerapkan rumus serta teknik analisis data. Oleh karena itu, pemilihan sumber belajar yang tepat sangat krusial. Berikut ini beberapa sumber belajar yang dapat digunakan untuk menemukan contoh soal statistika, beserta perbandingan keunggulan dan kekurangannya.
Berbagai Sumber Belajar Soal Statistika
Terdapat berbagai macam sumber belajar yang dapat dimanfaatkan untuk memperdalam pemahaman statistika melalui latihan soal. Mulai dari buku teks, website edukasi online, hingga aplikasi pembelajaran, masing-masing memiliki karakteristik dan keunggulan tersendiri.
- Buku Teks Statistika: Buku teks menawarkan penjelasan konsep yang sistematis dan terstruktur, disertai contoh soal dan latihan yang terintegrasi dengan materi. Keunggulannya adalah kedalaman materi dan penyajian yang komprehensif. Namun, kekurangannya adalah aksesibilitas yang terbatas dan mungkin kurang interaktif.
- Website Edukasi Online: Website seperti Khan Academy, Coursera, edX, dan lainnya menyediakan berbagai materi statistika, termasuk contoh soal dan kuis interaktif. Keunggulannya adalah aksesibilitas yang mudah dan fleksibilitas waktu belajar. Kekurangannya adalah kualitas materi yang bervariasi dan mungkin kurangnya bimbingan personal.
- Aplikasi Pembelajaran: Beberapa aplikasi mobile menawarkan latihan soal statistika dengan fitur-fitur interaktif seperti umpan balik instan dan penyesuaian tingkat kesulitan. Keunggulannya adalah portabilitas dan kemudahan akses. Kekurangannya adalah cakupan materi yang mungkin terbatas dan ketergantungan pada perangkat elektronik.
Rekomendasi Sumber Belajar untuk Pemula
Bagi pemula, buku teks statistika yang ditulis dengan bahasa sederhana dan dilengkapi contoh soal yang terstruktur sangat direkomendasikan. Website edukasi online juga bisa menjadi pelengkap yang baik untuk memahami konsep tertentu secara lebih interaktif. Kombinasi keduanya akan memberikan pengalaman belajar yang seimbang dan efektif.
Daftar Buku Teks Statistika yang Direkomendasikan
Pemilihan buku teks statistika yang tepat sangat bergantung pada latar belakang pendidikan dan tingkat pemahaman. Berikut beberapa rekomendasi buku teks statistika, dengan penjelasan singkat:
| Judul Buku | Penulis | Penjelasan Singkat |
|---|---|---|
| Statistika untuk Bisnis dan Ekonomi | (Contoh Penulis) | Buku ini cocok untuk pemula dengan contoh kasus yang relevan dengan dunia bisnis dan ekonomi. |
| Pengantar Statistika | (Contoh Penulis) | Buku ini memberikan pemahaman dasar statistika secara komprehensif dengan penjelasan yang mudah dipahami. |
| Statistika Inferensial | (Contoh Penulis) | Buku ini cocok bagi yang ingin mempelajari statistika inferensial lebih lanjut, meliputi pengujian hipotesis dan estimasi parameter. |
Contoh Teknik Penyelesaian Soal Statistika
Banyak teknik penyelesaian soal statistika, salah satunya adalah metode pengujian hipotesis. Metode ini digunakan untuk menguji suatu klaim atau hipotesis tentang suatu populasi berdasarkan data sampel.
Langkah-langkah umum dalam pengujian hipotesis meliputi: merumuskan hipotesis nol dan alternatif, menentukan tingkat signifikansi, memilih uji statistik yang tepat, menghitung statistik uji, dan mengambil kesimpulan berdasarkan nilai p-value.
Interpretasi Hasil Soal Statistika

Interpretasi hasil merupakan tahap krusial dalam analisis statistika. Kemampuan menginterpretasikan data secara tepat akan menentukan kesimpulan yang dihasilkan dan pengambilan keputusan yang tepat berdasarkan analisis tersebut. Tanpa interpretasi yang akurat, data statistik yang dikumpulkan akan menjadi tidak bermakna.
Pentingnya Interpretasi Hasil dalam Analisis Statistika
Interpretasi hasil tidak hanya sekedar menjelaskan angka-angka yang didapatkan dari perhitungan statistik. Interpretasi yang baik menghubungkan hasil analisis dengan konteks permasalahan yang diteliti, menjelaskan implikasi temuan, dan menjawab pertanyaan penelitian. Interpretasi yang tepat memungkinkan peneliti untuk menarik kesimpulan yang valid dan bermakna, serta memberikan rekomendasi yang relevan bagi pengambilan keputusan.
Contoh Soal dan Interpretasi Hasil
Misalnya, sebuah penelitian ingin mengetahui apakah ada perbedaan rata-rata tinggi badan antara siswa laki-laki dan perempuan di suatu sekolah. Setelah dilakukan pengumpulan data dan uji t-test independen, diperoleh nilai p = 0.02 dan t-hitung = 2.5. Dengan tingkat signifikansi 0.05, nilai p (0.02) lebih kecil dari tingkat signifikansi (0.05). Ini berarti terdapat perbedaan yang signifikan secara statistik antara rata-rata tinggi badan siswa laki-laki dan perempuan.
Nilai t-hitung (2.5) menunjukkan kekuatan perbedaan tersebut. Namun, perlu diingat bahwa signifikansi statistik tidak selalu berarti signifikansi praktis. Perbedaan rata-rata tinggi badan mungkin kecil dan tidak memiliki implikasi yang berarti dalam konteks kehidupan nyata.
Kesalahan Umum dalam Menginterpretasikan Hasil Statistika, Contoh soal statistika
Beberapa kesalahan umum yang sering terjadi antara lain: menganggap korelasi sebagai kausalitas (hanya karena dua variabel berkorelasi tidak berarti satu menyebabkan yang lain), mengabaikan ukuran efek (fokus hanya pada signifikansi statistik tanpa mempertimbangkan besarnya pengaruh), menginterpretasikan hasil di luar konteks penelitian, dan menarik kesimpulan yang terlalu umum berdasarkan sampel yang terbatas.
- Menyatakan hubungan sebab-akibat berdasarkan korelasi saja.
- Mengabaikan ukuran efek dan hanya berfokus pada signifikansi statistik.
- Menarik kesimpulan yang terlalu luas berdasarkan sampel yang kecil atau tidak representatif.
- Tidak mempertimbangkan faktor-faktor lain yang mungkin memengaruhi hasil.
Panduan Menulis Kesimpulan Berdasarkan Hasil Analisis Statistika
Kesimpulan yang baik harus ringkas, jelas, dan objektif. Kesimpulan harus mencerminkan hasil analisis statistik dan menjawab pertanyaan penelitian. Hindari interpretasi yang berlebihan atau spekulatif. Kesimpulan harus didukung oleh bukti empiris dan ditulis dengan bahasa yang mudah dipahami.
- Ringkasan singkat temuan utama.
- Penjelasan implikasi temuan terhadap pertanyaan penelitian.
- Pernyataan batasan penelitian dan saran untuk penelitian selanjutnya.
Kesalahan Interpretasi dan Pengambilan Keputusan
Kesalahan interpretasi data statistik dapat mengakibatkan pengambilan keputusan yang keliru, mengakibatkan kerugian finansial, kegagalan proyek, atau bahkan dampak negatif yang lebih serius. Oleh karena itu, pemahaman yang mendalam tentang metode statistika dan kemampuan menginterpretasikan hasil secara tepat sangat penting.
Ulasan Penutup
Mempelajari statistika membutuhkan latihan dan pemahaman konsep yang kuat. Dengan memahami berbagai jenis soal, menguasai teknik penyelesaian, dan mampu menginterpretasi hasil analisis dengan tepat, Anda akan siap menghadapi tantangan statistika di berbagai bidang. Semoga panduan ini bermanfaat dalam perjalanan belajar statistika Anda.