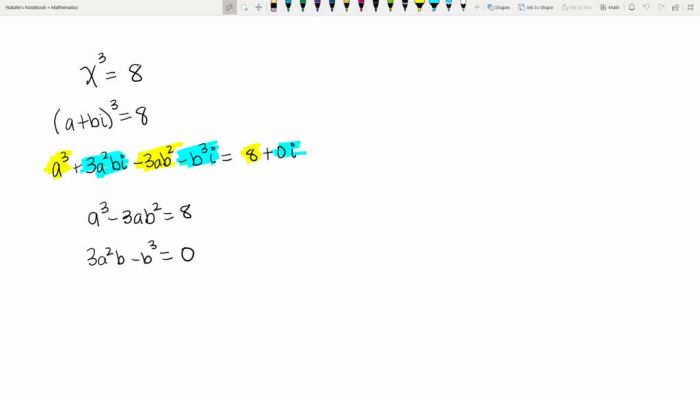
- Pengertian Induksi Matematika
- Langkah-langkah Pembuktian dengan Induksi Matematika
-
Contoh Soal Induksi Matematika dan Penyelesaiannya
- Contoh Soal Induksi Matematika Tingkat Mudah
- Contoh Soal Induksi Matematika Tingkat Sedang
- Contoh Soal Induksi Matematika Tingkat Sulit
- Ilustrasi Konsep Induksi Matematika
- Perbandingan Penyelesaian Tiga Contoh Soal, Contoh soal induksi matematika
- Contoh Soal Induksi Matematika yang Melibatkan Deret Geometri
- Kesalahan Umum dalam Pembuktian Induksi Matematika
- Penutupan Akhir
Contoh soal induksi matematika merupakan kunci menguasai metode pembuktian matematika yang elegan ini. Induksi matematika, berbeda dengan metode deduktif, membuktikan pernyataan benar untuk semua bilangan asli dengan cara membuktikan kebenaran untuk kasus dasar (basis induksi) dan kemudian menunjukkan bahwa jika pernyataan benar untuk suatu bilangan asli n, maka pernyataan juga benar untuk n+1 (langkah induksi). Memahami langkah-langkah ini sangat penting untuk menyelesaikan berbagai soal, mulai dari yang sederhana hingga yang kompleks.
Artikel ini akan membahas langkah-langkah pembuktian induksi matematika secara detail, disertai contoh soal dengan tingkat kesulitan bervariasi dan penjelasan penyelesaiannya. Dengan pemahaman yang komprehensif, diharapkan pembaca mampu mengaplikasikan metode ini dalam berbagai konteks matematika.
Pengertian Induksi Matematika

Induksi matematika merupakan metode pembuktian yang digunakan untuk menunjukkan kebenaran suatu pernyataan matematis untuk semua bilangan asli. Metode ini sangat efektif untuk membuktikan rumus atau teorema yang berlaku untuk sejumlah tak hingga anggota himpunan bilangan asli. Berbeda dengan metode pembuktian langsung yang memeriksa kebenaran pernyataan satu per satu, induksi matematika menggunakan prinsip dominan untuk membuktikan kebenaran pernyataan secara umum.
Meskipun terdengar rumit, prinsip induksi matematika sebenarnya cukup intuitif dan dapat dianalogikan dengan deretan domino. Jika kita ingin memastikan semua domino akan jatuh, kita hanya perlu memastikan dua hal: (1) domino pertama jatuh, dan (2) jika domino ke-n jatuh, maka domino ke-n+1 juga akan jatuh. Dengan begitu, kita dapat menyimpulkan bahwa semua domino akan jatuh, meskipun jumlahnya tak terhingga.
Contoh Penerapan Induksi Matematika dalam Kehidupan Sehari-hari
Analogi deretan domino di atas merupakan contoh sederhana penerapan induksi matematika. Contoh lain yang lebih konkret adalah menentukan jumlah uang yang terkumpul dalam celengan setiap harinya. Misalkan seseorang menabung Rp 1000 setiap hari. Pada hari pertama, jumlah uangnya Rp 1000. Jika kita berasumsi pada hari ke-n jumlah uangnya adalah Rp 1000n, maka pada hari ke-n+1 jumlah uangnya akan menjadi Rp 1000(n+1).
Dengan induksi matematika, kita dapat membuktikan bahwa pada hari ke-n, jumlah uang yang terkumpul selalu Rp 1000n.
Langkah-langkah Pembuktian dengan Induksi Matematika
Pembuktian dengan induksi matematika umumnya terdiri dari tiga langkah utama. Ketiga langkah ini harus dipenuhi agar pembuktian dinyatakan valid.
- Basis Induksi: Buktikan bahwa pernyataan tersebut benar untuk kasus dasar, biasanya n = 1.
- Hipotesis Induksi: Asumsikan bahwa pernyataan tersebut benar untuk suatu bilangan asli k (dengan k ≥ 1). Ini adalah langkah kunci dalam induksi matematika, di mana kita menganggap pernyataan benar untuk kasus umum.
- Langkah Induksi: Buktikan bahwa jika pernyataan tersebut benar untuk n = k (berdasarkan hipotesis induksi), maka pernyataan tersebut juga benar untuk n = k + 1. Ini menunjukkan bahwa kebenaran pernyataan untuk satu kasus akan mengimplikasikan kebenaran untuk kasus berikutnya.
Perbandingan Metode Pembuktian Langsung dan Induksi Matematika
Berikut tabel perbandingan metode pembuktian langsung dan induksi matematika:
| Metode Pembuktian | Kelebihan | Kekurangan | Contoh Penerapan |
|---|---|---|---|
| Pembuktian Langsung | Mudah dipahami untuk kasus sederhana; memberikan bukti yang jelas dan langsung. | Tidak efisien untuk pernyataan yang berlaku untuk semua bilangan asli; sulit diterapkan untuk kasus yang kompleks. | Membuktikan bahwa jumlah dua bilangan genap selalu genap. |
| Induksi Matematika | Efisien untuk membuktikan pernyataan untuk semua bilangan asli; metode yang sistematis dan terstruktur. | Membutuhkan pemahaman konseptual yang kuat; terkadang sulit menemukan langkah induksi. | Membuktikan rumus jumlah deret aritmatika. |
Perbedaan Prinsip Induksi Matematika dan Deduksi
Induksi matematika bergerak dari kasus khusus (basis induksi) menuju kesimpulan umum, sementara deduksi bergerak dari premis umum menuju kesimpulan khusus. Induksi matematika menggunakan prinsip domino, sementara deduksi menggunakan aturan logika untuk menarik kesimpulan. Induksi matematika bersifat probabilistik (walaupun sangat kuat), sedangkan deduksi bersifat deterministik. Kesimpulan dari induksi matematika dapat dianggap benar dengan tingkat kepercayaan yang tinggi, tetapi tidak sepenuhnya mutlak, sedangkan kesimpulan dari deduksi bersifat mutlak jika premisnya benar.
Langkah-langkah Pembuktian dengan Induksi Matematika
Induksi matematika merupakan teknik pembuktian yang sangat berguna untuk membuktikan pernyataan matematika yang berlaku untuk semua bilangan bulat positif. Metode ini didasarkan pada prinsip domino: jika kita dapat menjatuhkan domino pertama (basis induksi), dan jika jatuhnya setiap domino menyebabkan domino berikutnya jatuh (langkah induksi), maka semua domino akan jatuh.
Langkah-langkah Pembuktian Induksi Matematika
Pembuktian dengan induksi matematika terdiri dari dua langkah utama:
- Basis Induksi: Buktikan bahwa pernyataan tersebut benar untuk kasus terkecil (biasanya n = 1).
- Langkah Induksi: Asumsikan pernyataan tersebut benar untuk suatu bilangan bulat positif k (hipotesis induksi). Kemudian, buktikan bahwa pernyataan tersebut juga benar untuk k + 1.
Jika kedua langkah ini berhasil dibuktikan, maka pernyataan tersebut terbukti benar untuk semua bilangan bulat positif.
Contoh Langkah-langkah Pembuktian: Jumlah n Bilangan Bulat Pertama
Mari kita buktikan rumus jumlah n bilangan bulat pertama: 1 + 2 + 3 + … + n = n(n+1)/2 menggunakan induksi matematika.
- Basis Induksi (n = 1):
Pernyataan: 1 = 1(1+1)/2Bukti: 1 = 1. Pernyataan benar untuk n = 1.
- Langkah Induksi:
Asumsi (Hipotesis Induksi): Asumsikan pernyataan benar untuk n = k, yaitu 1 + 2 + 3 + … + k = k(k+1)/2.
Kita perlu membuktikan bahwa pernyataan juga benar untuk n = k + 1, yaitu 1 + 2 + 3 + … + k + (k+1) = (k+1)(k+2)/2.
Bukti: Mulai dari ruas kiri:+ 2 + 3 + … + k + (k+1) = k(k+1)/2 + (k+1) (menggunakan hipotesis induksi)= (k(k+1) + 2(k+1))/2= (k+1)(k+2)/2Ini sama dengan ruas kanan. Jadi, pernyataan benar untuk n = k + 1.
Karena pernyataan benar untuk n = 1 (basis induksi) dan jika benar untuk n = k maka juga benar untuk n = k + 1 (langkah induksi), maka berdasarkan prinsip induksi matematika, pernyataan tersebut benar untuk semua bilangan bulat positif n.
Diagram Alur Pembuktian Induksi Matematika
Diagram alur berikut ini menggambarkan langkah-langkah pembuktian induksi matematika:
- Mulai
- Basis Induksi: Buktikan pernyataan benar untuk n=1
- Langkah Induksi: Asumsikan pernyataan benar untuk n=k (Hipotesis Induksi)
- Buktikan pernyataan benar untuk n=k+1
- Kesimpulan: Pernyataan benar untuk semua bilangan bulat positif n
- Selesai
Contoh Soal Induksi Matematika dan Penyelesaiannya
Buktikan bahwa 1 + 3 + 5 + … + (2n – 1) = n² untuk semua bilangan bulat positif n.
- Basis Induksi (n = 1):
Pernyataan: 1 = 1²Bukti: 1 = 1. Pernyataan benar untuk n = 1.
- Langkah Induksi:
Asumsi (Hipotesis Induksi): Asumsikan pernyataan benar untuk n = k, yaitu 1 + 3 + 5 + … + (2k – 1) = k².
Kita perlu membuktikan bahwa pernyataan juga benar untuk n = k + 1, yaitu 1 + 3 + 5 + … + (2k – 1) + (2(k+1) – 1) = (k+1)².
Bukti: Mulai dari ruas kiri:
- + 3 + 5 + … + (2k – 1) + (2(k+1)
- 1) = k² + (2k + 1) (menggunakan hipotesis induksi)
= k² + 2k + 1= (k + 1)²Ini sama dengan ruas kanan. Jadi, pernyataan benar untuk n = k + 1.
Karena pernyataan benar untuk n = 1 dan jika benar untuk n = k maka juga benar untuk n = k + 1, maka berdasarkan prinsip induksi matematika, pernyataan tersebut benar untuk semua bilangan bulat positif n.
Contoh Soal Induksi Matematika dan Penyelesaiannya

Induksi matematika merupakan metode pembuktian yang sangat berguna dalam matematika, khususnya untuk membuktikan pernyataan yang berlaku untuk semua bilangan asli. Metode ini didasarkan pada prinsip domino: jika kita bisa menjatuhkan domino pertama, dan jika setiap domino menjatuhkan domino berikutnya, maka semua domino akan jatuh. Berikut beberapa contoh soal induksi matematika dengan tingkat kesulitan yang bervariasi, beserta penyelesaian langkah demi langkahnya.
Contoh Soal Induksi Matematika Tingkat Mudah
Buktikan bahwa 1 + 2 + 3 + … + n = n(n+1)/2 untuk semua bilangan asli n.
- Basis Induksi (n=1): Jika n = 1, maka ruas kiri adalah 1, dan ruas kanan adalah 1(1+1)/2 = 1. Pernyataan tersebut benar untuk n = 1.
- Hipotesis Induksi: Asumsikan pernyataan benar untuk suatu bilangan asli k, yaitu 1 + 2 + 3 + … + k = k(k+1)/2.
- Langkah Induksi: Kita perlu membuktikan bahwa pernyataan juga benar untuk n = k+1, yaitu 1 + 2 + 3 + … + k + (k+1) = (k+1)(k+2)/
Dengan menggunakan hipotesis induksi, kita dapat menulis:
- 1 + 2 + 3 + … + k + (k+1) = k(k+1)/2 + (k+1) = (k(k+1) + 2(k+1))/2 = (k+1)(k+2)/2.
- Karena pernyataan benar untuk n = k+1, maka berdasarkan prinsip induksi matematika, pernyataan tersebut benar untuk semua bilangan asli n.
Contoh Soal Induksi Matematika Tingkat Sedang
Buktikan bahwa n 3 + 2n merupakan bilangan kelipatan 3 untuk semua bilangan asli n.
- Basis Induksi (n=1): Jika n = 1, maka n 3 + 2n = 1 + 2 = 3, yang merupakan kelipatan 3. Pernyataan benar untuk n = 1.
- Hipotesis Induksi: Asumsikan pernyataan benar untuk suatu bilangan asli k, yaitu k 3 + 2k merupakan kelipatan 3. Artinya, k 3 + 2k = 3m untuk suatu bilangan bulat m.
- Langkah Induksi: Kita perlu membuktikan bahwa (k+1) 3 + 2(k+1) juga merupakan kelipatan
3. Kita perlu mengembangkan ekspresi tersebut
- (k+1) 3 + 2(k+1) = k 3 + 3k 2 + 3k + 1 + 2k + 2 = (k 3 + 2k) + 3k 2 + 3k + 3. Karena k 3 + 2k = 3m, maka ekspresi tersebut dapat ditulis sebagai 3m + 3k 2 + 3k + 3 = 3(m + k 2 + k + 1), yang jelas merupakan kelipatan 3.
- Karena pernyataan benar untuk n = k+1, maka berdasarkan prinsip induksi matematika, pernyataan tersebut benar untuk semua bilangan asli n.
Contoh Soal Induksi Matematika Tingkat Sulit
Buktikan bahwa untuk setiap bilangan asli n ≥ 2, berlaku 2 n > n 2.
- Basis Induksi (n=2): Jika n = 2, maka 2 2 = 4 dan 2 2 = 4. Pernyataan tersebut benar untuk n = 2 (walaupun tidak lebih besar, tetapi kita perlu memulai dari sini).
- Basis Induksi (n=3): Jika n = 3, maka 2 3 = 8 dan 3 2 = 9. Pernyataan salah untuk n=3, perlu dicek untuk n=4 dan seterusnya. Jika n=4, 2 4 = 16 > 16 (salah). Jika n=5, 2 5 = 32 > 25. Jadi kita akan mulai dari n=5.
- Basis Induksi (n=5): Jika n=5, 2 5 = 32 > 25 = 5 2. Pernyataan benar untuk n = 5.
- Hipotesis Induksi: Asumsikan pernyataan benar untuk suatu bilangan asli k ≥ 5, yaitu 2 k > k 2.
- Langkah Induksi: Kita perlu membuktikan bahwa 2 k+1 > (k+1) 2. Dari hipotesis induksi, kita kalikan kedua ruas dengan 2: 2 k+1 > 2k 2. Kita perlu menunjukkan bahwa 2k 2 > (k+1) 2 untuk k ≥ 5. Ini setara dengan 2k 2 > k 2 + 2k + 1, atau k 2 > 2k + 1. Untuk k ≥ 5, ini selalu benar (misalnya, untuk k=5, 25 > 11; untuk k=6, 36 > 13, dan seterusnya).
- Karena pernyataan benar untuk n = k+1, maka berdasarkan prinsip induksi matematika, pernyataan tersebut benar untuk semua bilangan asli n ≥ 5.
Ilustrasi Konsep Induksi Matematika
Bayangkan deretan domino yang tak terhingga jumlahnya. Bukti induksi matematika seperti menjatuhkan domino-domino tersebut. Contoh soal pertama (1 + 2 + 3 + … + n = n(n+1)/2) dapat diilustrasikan sebagai berikut: Domino pertama (n=1) jatuh karena 1 = 1(1+1)/2. Hipotesis induksi adalah asumsi bahwa domino ke-k jatuh (1 + 2 + …
+ k = k(k+1)/2). Langkah induksi membuktikan bahwa jika domino ke-k jatuh, maka domino ke-(k+1) juga akan jatuh (karena kita menunjukkan bahwa 1 + 2 + … + k + (k+1) = (k+1)(k+2)/2). Karena domino pertama jatuh dan setiap domino menjatuhkan domino berikutnya, maka semua domino akan jatuh, artinya pernyataan tersebut benar untuk semua bilangan asli n.
Perbandingan Penyelesaian Tiga Contoh Soal, Contoh soal induksi matematika
Ketiga contoh soal tersebut menggunakan prinsip induksi matematika yang sama, namun tingkat kesulitannya berbeda. Soal pertama relatif mudah karena langkah induksinya langsung. Soal kedua membutuhkan sedikit manipulasi aljabar untuk menunjukkan kelipatan 3. Soal ketiga merupakan yang paling menantang, membutuhkan analisis tambahan untuk membuktikan bahwa 2k 2 > (k+1) 2 untuk k ≥ 5. Perbedaan utama terletak pada kompleksitas aljabar dan penalaran yang dibutuhkan dalam langkah induksi.
Contoh Soal Induksi Matematika yang Melibatkan Deret Geometri
Buktikan bahwa jumlah deret geometri 1 + r + r 2 + … + r n = (1 – r n+1)/(1 – r) untuk semua bilangan asli n dan r ≠ 1.
- Basis Induksi (n=1): Jika n = 1, maka ruas kiri adalah 1 + r, dan ruas kanan adalah (1 – r 2)/(1 – r) = (1 – r)(1 + r)/(1 – r) = 1 + r. Pernyataan benar untuk n = 1.
- Hipotesis Induksi: Asumsikan pernyataan benar untuk suatu bilangan asli k, yaitu 1 + r + r 2 + … + r k = (1 – r k+1)/(1 – r).
- Langkah Induksi: Kita perlu membuktikan bahwa 1 + r + r 2 + … + r k + r k+1 = (1 – r k+2)/(1 – r). Dengan menggunakan hipotesis induksi:
- (1 – r k+1)/(1 – r) + r k+1 = (1 – r k+1 + r k+1(1 – r))/(1 – r) = (1 – r k+1 + r k+1
rk+2)/(1 – r) = (1 – r k+2)/(1 – r).
- Karena pernyataan benar untuk n = k+1, maka berdasarkan prinsip induksi matematika, pernyataan tersebut benar untuk semua bilangan asli n dan r ≠ 1.
Kesalahan Umum dalam Pembuktian Induksi Matematika
Pembuktian induksi matematika, meskipun tampak sederhana, seringkali menyimpan jebakan bagi pemula. Kesalahan kecil dapat mengakibatkan kesimpulan yang salah, meskipun langkah-langkah awalnya tampak benar. Memahami kesalahan umum ini penting untuk memastikan validitas pembuktian. Artikel ini akan mengidentifikasi beberapa kesalahan tersebut, memberikan contoh, dan menawarkan panduan untuk menghindari kesalahan serupa di masa mendatang.
Salah satu tantangan utama dalam induksi matematika adalah memastikan setiap langkah logis dan terhubung dengan benar. Kesalahan seringkali muncul karena kurangnya ketelitian atau pemahaman yang kurang mendalam terhadap prinsip-prinsip dasar induksi matematika. Dengan memahami kesalahan-kesalahan umum ini, kita dapat meningkatkan akurasi dan kepercayaan diri dalam melakukan pembuktian.
Contoh Kesalahan Umum dalam Langkah Basis
Langkah basis, yaitu membuktikan pernyataan benar untuk n=1 (atau nilai awal lainnya), merupakan fondasi pembuktian induksi. Kesalahan sering terjadi di sini karena kurangnya ketelitian dalam substitusi atau manipulasi aljabar. Misalnya, jika kita ingin membuktikan ∑ i=1n i = n(n+1)/2, kesalahan umum adalah hanya mengasumsikan kebenaran pernyataan tanpa melakukan substitusi n=1 secara eksplisit. Perlu ditunjukkan bahwa ∑ i=11 i = 1(1+1)/2 = 1, yang benar.
Mengabaikan langkah ini dapat membatalkan seluruh pembuktian.
Contoh Kesalahan Umum dalam Langkah Induksi
Langkah induksi, yaitu membuktikan bahwa jika pernyataan benar untuk n=k, maka pernyataan juga benar untuk n=k+1, membutuhkan manipulasi aljabar yang cermat. Kesalahan sering terjadi pada saat mengasumsikan kebenaran pernyataan untuk n=k dan kemudian mencoba membuktikan kebenarannya untuk n=k+1. Kesalahan umum lainnya adalah tidak secara tepat menghubungkan pernyataan untuk n=k dengan pernyataan untuk n=k+1. Contohnya, jika kita gagal menggunakan hipotesis induksi (pernyataan untuk n=k) secara tepat dalam pembuktian untuk n=k+1, maka argumen kita menjadi tidak valid.
Contoh Soal Induksi Matematika yang Salah dan Analisis Kesalahannya
Misalkan kita ingin membuktikan bahwa semua bilangan bulat positif adalah genap menggunakan induksi matematika.
- Langkah Basis: Untuk n=1, 1 adalah genap (SALAH).
- Langkah Induksi: Asumsikan bahwa k adalah genap, artinya k=2m untuk suatu bilangan bulat m. Maka k+1 = 2m+1, yang ganjil. Jadi, jika k genap, k+1 tidak selalu genap (SALAH). Kesimpulannya, argumen ini gagal karena langkah basis sudah salah.
Kesalahan utama terletak pada langkah basis yang salah. Angka 1 bukan bilangan genap. Langkah induksi, meskipun terlihat logis, tidak dapat menyelamatkan pembuktian yang sudah salah dari awal.
Cara Menghindari Kesalahan Umum
Untuk menghindari kesalahan, penting untuk:
- Memeriksa langkah basis dengan teliti dan memastikan pernyataan benar untuk nilai awal n.
- Menuliskan hipotesis induksi (pernyataan untuk n=k) dengan jelas dan menggunakannya secara tepat dalam langkah induksi.
- Menunjukkan dengan jelas bagaimana pernyataan untuk n=k+1 diturunkan dari pernyataan untuk n=k.
- Memeriksa kembali semua langkah aljabar dan manipulasi matematika untuk memastikan tidak ada kesalahan.
Tabel Kesalahan Umum dan Cara Mengatasinya
| Kesalahan | Deskripsi | Cara Mengatasi | Contoh |
|---|---|---|---|
| Langkah Basis Salah | Pernyataan tidak benar untuk nilai awal n. | Verifikasi langkah basis dengan cermat. | Mengasumsikan 1 adalah genap. |
| Penggunaan Hipotesis Induksi yang Salah | Hipotesis induksi tidak digunakan dengan tepat dalam langkah induksi. | Pastikan hipotesis induksi digunakan secara eksplisit dalam pembuktian untuk n=k+1. | Mencoba membuktikan n=k+1 tanpa menggunakan informasi bahwa n=k benar. |
| Kesalahan Aljabar | Kesalahan dalam manipulasi aljabar atau kalkulus. | Periksa kembali semua langkah aljabar dengan teliti. | Kesalahan dalam penyederhanaan ekspresi. |
Panduan Singkat untuk Memeriksa Kembali Pembuktian Induksi Matematika
- Ulangi langkah basis: Pastikan pernyataan benar untuk nilai awal n.
- Periksa hipotesis induksi: Pastikan Anda menggunakan hipotesis induksi (pernyataan untuk n=k) secara tepat dalam langkah induksi.
- Verifikasi langkah induksi: Pastikan Anda telah menunjukkan dengan jelas bagaimana pernyataan untuk n=k+1 diturunkan dari pernyataan untuk n=k.
- Tinjau kembali aljabar: Periksa kembali semua langkah aljabar dan pastikan tidak ada kesalahan.
- Baca ulang seluruh pembuktian: Setelah menyelesaikan pembuktian, bacalah kembali seluruh proses untuk memastikan logika dan aljabar Anda benar.
Penutupan Akhir

Induksi matematika terbukti menjadi alat yang ampuh dalam membuktikan berbagai pernyataan matematika yang berkaitan dengan bilangan asli. Mempelajari contoh soal dan memahami langkah-langkah pembuktian, termasuk menghindari kesalahan umum, merupakan kunci untuk menguasai teknik ini. Dengan latihan yang cukup, kemampuan untuk memecahkan soal induksi matematika akan semakin terasah, membuka jalan untuk eksplorasi lebih lanjut dalam dunia matematika.