Contoh soal barisan dan deret aritmatika merupakan kunci untuk memahami konsep matematika ini. Barisan dan deret aritmatika, dengan pola penjumlahan atau pengurangan yang konstan, seringkali muncul dalam kehidupan sehari-hari, mulai dari menabung hingga perencanaan proyek. Memahami konsep ini membuka pintu untuk menyelesaikan berbagai permasalahan, baik yang sederhana maupun kompleks. Artikel ini akan memberikan pemahaman yang komprehensif melalui penjelasan, contoh soal, dan penyelesaiannya.
Materi ini akan membahas definisi barisan dan deret aritmatika, perbedaan keduanya, rumus-rumus yang terkait, serta penerapannya dalam berbagai contoh soal dengan tingkat kesulitan yang bervariasi. Dengan langkah-langkah penyelesaian yang detail, diharapkan pembaca dapat memahami konsep dan mengaplikasikannya dengan mudah. Selain itu, akan dibahas juga penerapan barisan dan deret aritmatika dalam konteks kehidupan nyata.
Pengertian Barisan dan Deret Aritmatika
Barisan dan deret aritmatika merupakan konsep dasar dalam matematika yang berkaitan dengan urutan angka yang memiliki pola tertentu. Memahami keduanya sangat penting karena sering diterapkan dalam berbagai bidang, mulai dari perhitungan keuangan hingga perencanaan proyek. Pada artikel ini, kita akan membahas definisi, rumus, dan contoh soal dari barisan dan deret aritmatika.
Definisi Barisan Aritmatika dan Contohnya
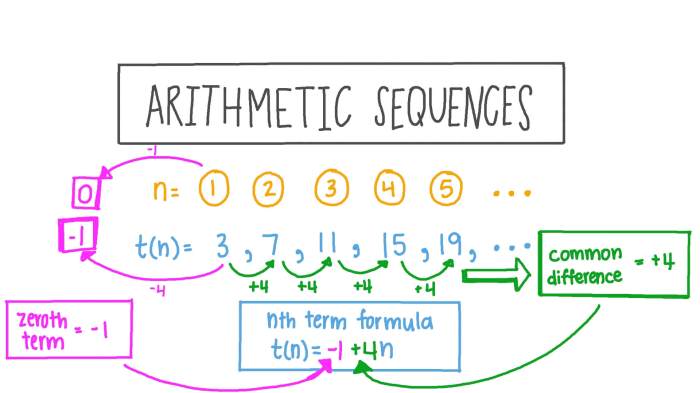
Barisan aritmatika adalah suatu barisan bilangan yang memiliki selisih tetap antara dua suku berurutan. Selisih tetap ini disebut beda (b). Dengan kata lain, setiap suku diperoleh dengan menambahkan beda (b) ke suku sebelumnya. Contohnya adalah barisan 2, 5, 8, 11, 14, … di mana bedanya adalah 3 (5-2=3, 8-5=3, dan seterusnya).
Definisi Deret Aritmatika dan Contohnya
Deret aritmatika adalah jumlah dari suku-suku dalam barisan aritmatika. Jika kita menjumlahkan suku-suku barisan aritmatika 2, 5, 8, 11, 14, maka kita mendapatkan deret aritmatika 2 + 5 + 8 + 11 + 14 =
40. Perbedaan utama dengan barisan aritmatika terletak pada hasil akhirnya: barisan menampilkan urutan angka, sementara deret menampilkan jumlah dari urutan tersebut.
Perbandingan Barisan dan Deret Aritmatika
Berikut tabel perbandingan antara barisan dan deret aritmatika:
| Nama | Definisi | Rumus Umum | Contoh |
|---|---|---|---|
| Barisan Aritmatika | Urutan bilangan dengan selisih tetap antara dua suku berurutan. | Un = a + (n-1)b | 2, 5, 8, 11, 14,… (a=2, b=3) |
| Deret Aritmatika | Jumlah suku-suku dalam barisan aritmatika. | Sn = n/2 (2a + (n-1)b) | 2 + 5 + 8 + 11 + 14 = 40 |
Keterangan: U n = suku ke-n, a = suku pertama, b = beda, n = banyak suku, S n = jumlah n suku pertama.
Contoh Soal Cerita Barisan dan Deret Aritmatika
Seorang pekerja bangunan menumpuk batu bata. Pada hari pertama, ia menumpuk 10 batu bata. Setiap hari berikutnya, ia menumpuk 5 batu bata lebih banyak daripada hari sebelumnya. Berapa banyak batu bata yang ditumpuk pekerja tersebut setelah 7 hari? Ini merupakan contoh soal deret aritmatika.
Untuk menyelesaikannya, kita dapat menggunakan rumus deret aritmatika dengan a = 10, b = 5, dan n = 7.
Contoh lain: Seorang anak menabung setiap minggu. Minggu pertama ia menabung Rp 10.000, minggu kedua Rp 12.000, dan seterusnya dengan kenaikan Rp 2.000 setiap minggunya. Berapakah jumlah tabungan anak tersebut setelah 10 minggu? Ini juga merupakan contoh soal deret aritmatika, dengan a = 10000, b = 2000, dan n = 10.
Perbedaan Utama Barisan dan Deret Aritmatika dalam Penyelesaian Masalah, Contoh soal barisan dan deret aritmatika
Perbedaan utama terletak pada apa yang dicari. Barisan aritmatika fokus pada urutan angka itu sendiri (misalnya, mencari suku ke-10), sedangkan deret aritmatika berfokus pada jumlah dari urutan angka tersebut (misalnya, mencari total tabungan selama 10 minggu). Oleh karena itu, rumus dan pendekatan penyelesaian masalahnya pun berbeda.
Rumus Barisan dan Deret Aritmatika
Barisan dan deret aritmatika merupakan konsep dasar dalam matematika yang membahas pola bilangan dengan selisih tetap antara dua suku berurutan. Memahami rumus-rumus yang terkait sangat penting untuk menyelesaikan berbagai permasalahan yang melibatkan pola bilangan ini. Berikut penjelasan rinci mengenai rumus-rumus tersebut beserta contoh penerapannya.
Rumus Suku ke-n Barisan Aritmatika
Rumus suku ke-n barisan aritmatika digunakan untuk menentukan nilai suatu suku tertentu dalam barisan tersebut tanpa harus menghitung semua suku sebelumnya. Rumus ini dinyatakan sebagai:
Un = a + (n-1)b
di mana:
- Un = suku ke-n
- a = suku pertama
- n = banyaknya suku
- b = beda (selisih antara dua suku berurutan)
Contoh Penerapan Rumus Suku ke-n Barisan Aritmatika
Misalnya, kita memiliki barisan aritmatika 2, 5, 8, 11, … Kita ingin mencari suku ke-10 (U 10). Dari barisan tersebut, kita dapat menentukan a = 2 dan b = 5 – 2 =
3. Dengan menggunakan rumus Un = a + (n-1)b, kita dapat menghitung U 10 sebagai berikut:
- U10 = 2 + (10 – 1)3
- U 10 = 2 + (9)3
- U 10 = 2 + 27
- U 10 = 29
Jadi, suku ke-10 dari barisan aritmatika tersebut adalah 29.
Rumus Jumlah n Suku Pertama Deret Aritmatika
Rumus jumlah n suku pertama deret aritmatika digunakan untuk menghitung total nilai dari n suku pertama suatu deret aritmatika. Rumus ini dinyatakan sebagai:
Sn = n/2 (2a + (n-1)b) atau Sn = n/2 (a + Un)
di mana:
- Sn = jumlah n suku pertama
- a = suku pertama
- n = banyaknya suku
- b = beda (selisih antara dua suku berurutan)
- Un = suku ke-n
Contoh Penerapan Rumus Jumlah n Suku Pertama Deret Aritmatika
Menggunakan barisan aritmatika yang sama (2, 5, 8, 11, …), kita ingin mencari jumlah 10 suku pertama (S 10). Kita sudah mengetahui a = 2, b = 3, dan dari perhitungan sebelumnya, U 10 =
29. Kita dapat menggunakan rumus S n = n/2 (a + U n) untuk menghitung S 10:
- S10 = 10/2 (2 + 29)
- S 10 = 5 (31)
- S 10 = 155
Jadi, jumlah 10 suku pertama dari deret aritmatika tersebut adalah 155.
Contoh Soal Gabungan Rumus Suku ke-n dan Jumlah n Suku Pertama
Sebuah barisan aritmatika memiliki suku ke-5 adalah 17 dan suku ke-10 adalah 32. Tentukan jumlah 20 suku pertama barisan tersebut.
Penyelesaian:
- Tentukan nilai a dan b. Kita memiliki dua persamaan:
- U5 = a + 4b = 17
- U 10 = a + 9b = 32
Dengan menyelesaikan sistem persamaan tersebut (misalnya dengan eliminasi atau substitusi), kita peroleh a = 1 dan b = 4.
- Hitung jumlah 20 suku pertama (S 20) menggunakan rumus S n = n/2 (2a + (n-1)b):
- S 20 = 20/2 (2(1) + (20-1)4)
- S 20 = 10 (2 + 76)
- S 20 = 780
Jadi, jumlah 20 suku pertama barisan aritmatika tersebut adalah 780.
Contoh Soal dan Penyelesaian Barisan Aritmatika: Contoh Soal Barisan Dan Deret Aritmatika

Barisan aritmatika merupakan barisan bilangan yang memiliki selisih tetap antara dua suku berurutan. Selisih tetap ini disebut beda (b). Memahami barisan aritmatika sangat penting dalam berbagai bidang, mulai dari perhitungan keuangan hingga penyelesaian masalah dalam ilmu fisika. Berikut ini beberapa contoh soal barisan aritmatika dengan tingkat kesulitan yang bervariasi, lengkap dengan penyelesaian langkah demi langkah.
Contoh Soal Barisan Aritmatika Tingkat Mudah
Suatu barisan aritmatika memiliki suku pertama 2 dan beda 3. Tentukan suku ke-5 barisan tersebut.
Penyelesaian:
Rumus umum suku ke-n barisan aritmatika adalah Un = a + (n-1)b, dengan a = suku pertama, b = beda, dan n = banyak suku. Dalam soal ini, a = 2, b = 3, dan n = 5. Substitusikan nilai-nilai tersebut ke dalam rumus untuk mendapatkan suku ke-5.
Langkah 1: Substitusikan nilai a, b, dan n ke dalam rumus Un = a + (n-1)b.
Langkah 2: U5 = 2 + (5-1)3 = 2 + 12 = 14
Jadi, suku ke-5 barisan aritmatika tersebut adalah 14.
Identifikasi pola: Barisan tersebut adalah 2, 5, 8, 11, 14,… Dengan mudah kita dapat melihat bahwa setiap suku bertambah 3 dari suku sebelumnya.
Contoh Soal Barisan Aritmatika Tingkat Sedang
Suku ke-3 dan suku ke-8 suatu barisan aritmatika berturut-turut adalah 11 dan 26. Tentukan suku pertama dan beda barisan tersebut.
Penyelesaian:
Kita dapat membentuk dua persamaan linear dengan menggunakan rumus suku ke-n barisan aritmatika. Kemudian, selesaikan sistem persamaan tersebut untuk mencari nilai a (suku pertama) dan b (beda).
Langkah 1: Buat dua persamaan berdasarkan informasi yang diberikan:
U3 = a + 2b = 11
U8 = a + 7b = 26
Langkah 2: Kurangkan persamaan pertama dari persamaan kedua untuk mengeliminasi a:
5b = 15 => b = 3
Langkah 3: Substitusikan nilai b ke salah satu persamaan untuk mencari a:
a + 2(3) = 11 => a = 5
Jadi, suku pertama (a) adalah 5 dan beda (b) adalah 3.
Contoh Soal Barisan Aritmatika Tingkat Sulit
Jumlah n suku pertama suatu barisan aritmatika adalah Sn = 2n² + 3n. Tentukan suku ke-10 barisan tersebut.
Penyelesaian:
Gunakan rumus jumlah n suku pertama barisan aritmatika (Sn) dan rumus suku ke-n (Un) untuk menyelesaikan soal ini. Perhatikan hubungan antara Sn dan Un.
Langkah 1: Rumus jumlah n suku pertama barisan aritmatika adalah Sn = n/2 (2a + (n-1)b). Kita memiliki Sn = 2n² + 3n. Kita dapat mencari U1 dan b dengan membandingkan kedua rumus ini.
Langkah 2: Untuk n=1, S1 = U1 = 2(1)² + 3(1) = 5. Jadi, a = 5.
Langkah 3: Untuk n=2, S2 = U1 + U2 = 2(2)² + 3(2) = 14. Karena U1 = 5, maka U2 = 14 – 5 = 9. Beda (b) = U2 – U1 = 9 – 5 = 4.
Langkah 4: Gunakan rumus Un = a + (n-1)b untuk mencari U10:
U10 = 5 + (10-1)4 = 5 + 36 = 41
Jadi, suku ke-10 barisan aritmatika tersebut adalah 41.
Contoh Soal dan Penyelesaian Deret Aritmatika

Setelah memahami konsep barisan dan deret aritmatika, mari kita praktikkan dengan beberapa contoh soal. Contoh-contoh soal berikut ini akan membantu Anda menguasai perhitungan deret aritmatika dengan tingkat kesulitan yang bervariasi, mulai dari mudah hingga sulit. Penyelesaian setiap soal akan dijabarkan langkah demi langkah, disertai dengan penjelasan strategi yang digunakan.
Pemahaman yang kuat tentang rumus dan penerapannya sangat penting dalam menyelesaikan soal deret aritmatika. Dengan latihan yang cukup, Anda akan mampu menyelesaikan soal-soal yang lebih kompleks dengan mudah dan efisien.
Contoh Soal Deret Aritmatika Mudah
Sebuah deret aritmatika memiliki suku pertama a = 2 dan beda b = 3. Tentukan jumlah 5 suku pertama deret tersebut.
Penyelesaian:
Rumus jumlah n suku pertama deret aritmatika adalah: Sn = n/2 (2a + (n-1)b). Dalam kasus ini, n = 5, a = 2, dan b = 3. Substitusikan nilai-nilai tersebut ke dalam rumus untuk mendapatkan jumlah 5 suku pertama.
Langkah 1: Substitusikan nilai n, a, dan b ke dalam rumus: S 5 = 5/2 (2(2) + (5-1)(3))
Langkah 2: Hitung operasi dalam kurung: S 5 = 5/2 (4 + 12)
Langkah 3: Hitung hasil perkalian dan pembagian: S 5 = 5/2 (16) = 40
Jadi, jumlah 5 suku pertama deret aritmatika tersebut adalah 40.
Contoh Soal Deret Aritmatika Sedang
Jumlah 10 suku pertama suatu deret aritmatika adalah 200, dan suku ke-10 adalah 38. Tentukan suku pertama (a) dan beda (b) deret tersebut.
Penyelesaian:
Kita akan menggunakan dua rumus: rumus jumlah n suku pertama (Sn = n/2 (2a + (n-1)b)) dan rumus suku ke-n (U n = a + (n-1)b). Kita memiliki dua persamaan dengan dua variabel (a dan b), sehingga kita dapat menyelesaikannya secara simultan.
Langkah 1: Gunakan rumus S n: 200 = 10/2 (2a + (10-1)b) => 200 = 5(2a + 9b) => 40 = 2a + 9b
Langkah 2: Gunakan rumus U n: 38 = a + (10-1)b => 38 = a + 9b
Langkah 3: Selesaikan sistem persamaan linear: Kita punya 40 = 2a + 9b dan 38 = a + 9b. Kurangi persamaan kedua dari persamaan pertama: 2 = a. Substitusikan a = 2 ke dalam persamaan kedua: 38 = 2 + 9b => 36 = 9b => b = 4.
Jadi, suku pertama (a) adalah 2 dan beda (b) adalah 4.
Contoh Soal Deret Aritmatika Sulit
Jumlah suku-suku genap dari deret aritmatika 2, 5, 8, 11, … sampai suku ke-20 adalah …
Penyelesaian:
Soal ini membutuhkan sedikit manipulasi. Kita perlu menemukan pola dari suku-suku genap, kemudian menghitung jumlahnya. Perhatikan bahwa suku-suku genap membentuk deret aritmatika baru.
Langkah 1: Tentukan pola suku genap: Suku genap adalah 2, 8, 14, … Ini membentuk deret aritmatika dengan a = 2 dan b = 6.
Langkah 2: Tentukan banyaknya suku genap: Karena deret aslinya memiliki 20 suku, maka deret suku genap memiliki 10 suku (20/2 = 10).
Langkah 3: Gunakan rumus jumlah n suku pertama: S 10 = 10/2 (2(2) + (10-1)(6)) = 5(4 + 54) = 5(58) = 290
Jadi, jumlah suku-suku genap dari deret aritmatika tersebut sampai suku ke-20 adalah 290.
Ilustrasi Deskriptif Soal Deret Aritmatika Mudah
Bayangkan Anda menumpuk balok-balok kayu. Pada tumpukan pertama, Anda meletakkan 2 balok. Pada tumpukan kedua, Anda menambahkan 3 balok lagi (total 5 balok). Pada tumpukan ketiga, Anda menambahkan 3 balok lagi (total 8 balok), dan seterusnya. Setiap tumpukan mewakili suku dalam deret aritmatika dengan a = 2 dan b = 3.
Jumlah balok pada kelima tumpukan pertama (jumlah 5 suku pertama) dapat divisualisasikan sebagai total balok yang digunakan dalam kelima tumpukan tersebut. Dengan menghitung jumlah balok pada setiap tumpukan dan menjumlahkannya, kita mendapatkan total 40 balok, yang sama dengan hasil perhitungan menggunakan rumus deret aritmatika.
Penerapan Barisan dan Deret Aritmatika dalam Kehidupan Sehari-hari

Barisan dan deret aritmatika, meskipun terlihat seperti konsep matematika abstrak, sebenarnya memiliki penerapan yang luas dalam kehidupan sehari-hari. Konsep ini membantu kita dalam menganalisis dan memprediksi pola numerik yang berulang, memudahkan pengambilan keputusan yang lebih terinformasi, dan bahkan membantu dalam perencanaan keuangan.
Pemahaman tentang barisan dan deret aritmatika memungkinkan kita untuk memodelkan situasi yang melibatkan penambahan atau pengurangan konstan, sehingga kita dapat memprediksi nilai-nilai di masa mendatang atau menghitung jumlah total dari suatu rangkaian peristiwa.
Contoh Penerapan Barisan dan Deret Aritmatika
Berikut beberapa contoh penerapan barisan dan deret aritmatika dalam kehidupan sehari-hari, dijelaskan bagaimana konsep tersebut digunakan, serta pentingnya pemahaman tersebut dalam pengambilan keputusan.
- Menabung Secara Berkala: Misalnya, seseorang menabung sebesar Rp 100.000 setiap bulan. Jumlah tabungannya setiap bulan membentuk barisan aritmatika dengan beda (selisih antar suku) sebesar Rp 100.000. Dengan menggunakan rumus deret aritmatika, kita dapat menghitung total tabungan setelah beberapa bulan tertentu. Pemahaman ini penting untuk merencanakan pengeluaran dan mencapai target keuangan.
- Susunan Kursi di Aula: Bayangkan sebuah aula dengan kursi yang disusun sedemikian rupa sehingga baris pertama terdapat 10 kursi, baris kedua 12 kursi, baris ketiga 14 kursi, dan seterusnya. Susunan kursi ini membentuk barisan aritmatika dengan beda 2. Dengan menggunakan rumus barisan aritmatika, kita dapat menghitung jumlah kursi pada baris tertentu atau total jumlah kursi di aula tersebut. Informasi ini penting untuk merencanakan kapasitas ruangan dan pengaturan tempat duduk.
- Pertambahan Tinggi Tanaman: Sebuah tanaman tumbuh dengan laju konstan, misalnya 2 cm per minggu. Tinggi tanaman setiap minggunya membentuk barisan aritmatika. Dengan mengetahui tinggi awal dan laju pertumbuhan, kita dapat memprediksi tinggi tanaman pada minggu-minggu berikutnya. Informasi ini berguna dalam pertanian dan hortikultura untuk memantau pertumbuhan tanaman dan mengoptimalkan perawatan.
Skenario Masalah Kehidupan Nyata dan Penyelesaiannya
Sebuah perusahaan merencanakan untuk meningkatkan produksi barangnya setiap bulan. Pada bulan pertama, mereka memproduksi 1000 unit barang. Setiap bulan berikutnya, produksi ditingkatkan sebesar 200 unit. Berapa total produksi barang selama 6 bulan pertama?
- Identifikasi Pola: Produksi barang membentuk barisan aritmatika dengan suku pertama (a) = 1000 dan beda (b) = 200.
- Tentukan Jumlah Suku: Jumlah bulan yang akan dihitung adalah 6 bulan (n = 6).
- Gunakan Rumus Deret Aritmatika: Rumus untuk mencari jumlah n suku pertama deret aritmatika adalah
Sn = n/2 [2a + (n-1)b]
. - Hitung Total Produksi: Substitusikan nilai a, b, dan n ke dalam rumus: S6 = 6/2 [2(1000) + (6-1)200] = 3 [2000 + 1000] = 9000.
- Kesimpulan: Total produksi barang selama 6 bulan pertama adalah 9000 unit.
Ulasan Penutup
Setelah mempelajari contoh soal barisan dan deret aritmatika beserta penyelesaiannya, diharapkan pemahaman mengenai konsep barisan dan deret aritmatika semakin mantap. Kemampuan untuk mengidentifikasi pola, mengaplikasikan rumus dengan tepat, dan menganalisis masalah merupakan kunci dalam menguasai materi ini. Dengan latihan yang konsisten, penggunaan barisan dan deret aritmatika dalam memecahkan masalah, baik dalam konteks akademis maupun kehidupan sehari-hari, akan menjadi lebih mudah dan efektif.