- Pengertian Perbandingan Senilai
-
Cara Menyelesaikan Soal Perbandingan Senilai
- Menyelesaikan Soal Perbandingan Senilai yang Melibatkan Tiga Besaran
- Contoh Soal Cerita Perbandingan Senilai yang Kompleks dan Penyelesaiannya
- Metode Proporsi dalam Menyelesaikan Soal Perbandingan Senilai
- Contoh Soal Perbandingan Senilai yang Melibatkan Skala Peta dan Solusinya
- Langkah-langkah Menyelesaikan Soal Perbandingan Senilai dengan Metode Perbandingan
-
Penerapan Perbandingan Senilai dalam Kehidupan Nyata: Contoh Perbandingan Senilai
- Penerapan Perbandingan Senilai dalam Bidang Ekonomi
- Perbandingan Senilai dalam Perencanaan Pembangunan Infrastruktur
- Penentuan Harga Jual Produk Berdasarkan Biaya Produksi dan Keuntungan
- Penerapan Perbandingan Senilai dalam Bidang Kesehatan: Perhitungan Dosis Obat
- Penentuan Rasio Campuran Bahan Bangunan, Contoh perbandingan senilai
- Contoh Soal dan Pembahasan Perbandingan Senilai
- Pemungkas
Contoh perbandingan senilai merupakan konsep matematika fundamental yang sering kita temui dalam kehidupan sehari-hari. Dari menghitung bahan kue hingga merencanakan perjalanan, pemahaman tentang perbandingan senilai sangatlah penting. Artikel ini akan menjelajahi pengertian perbandingan senilai, cara menyelesaikan soal, penerapannya dalam berbagai bidang, serta contoh soal dan pembahasannya secara rinci, sehingga Anda dapat menguasai konsep ini dengan mudah.
Kita akan mulai dengan definisi dasar perbandingan senilai, lalu mempelajari berbagai metode penyelesaian soal, mulai dari yang sederhana hingga yang kompleks. Selanjutnya, kita akan melihat bagaimana perbandingan senilai diterapkan dalam berbagai konteks, seperti ekonomi, pembangunan infrastruktur, dan bahkan kesehatan. Dengan contoh-contoh soal yang beragam dan pembahasan langkah demi langkah, Anda akan siap menghadapi berbagai tantangan yang melibatkan perbandingan senilai.
Pengertian Perbandingan Senilai
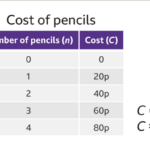
Perbandingan senilai merupakan hubungan antara dua besaran yang saling bergantung, di mana jika salah satu besaran bertambah, maka besaran lainnya juga akan bertambah secara proporsional. Sebaliknya, jika salah satu besaran berkurang, maka besaran lainnya juga akan berkurang secara proporsional. Konsep ini sering dijumpai dalam kehidupan sehari-hari dan menjadi dasar dalam berbagai perhitungan.
Contoh Perbandingan Senilai dalam Kehidupan Sehari-hari
Contoh sederhana perbandingan senilai adalah hubungan antara jumlah barang yang dibeli dengan total harga yang harus dibayar. Semakin banyak barang yang dibeli, semakin besar pula total harga yang harus dibayar, dengan asumsi harga per unit barang tetap sama. Contoh lain adalah hubungan antara jumlah jam kerja dengan total upah yang diterima, semakin banyak jam kerja, semakin besar upah yang diterima (dengan asumsi upah per jam tetap).
Ilustrasi Perbandingan Senilai: Kecepatan dan Jarak Tempuh
Bayangkan sebuah mobil yang melaju dengan kecepatan konstan. Jika kecepatan mobil tersebut tetap 60 km/jam, maka jarak yang ditempuh akan berbanding lurus dengan waktu tempuh. Artinya, jika mobil tersebut melaju selama 2 jam, maka jarak yang ditempuh adalah 120 km (60 km/jam x 2 jam). Jika waktu tempuh diperpanjang menjadi 3 jam, maka jarak yang ditempuh menjadi 180 km (60 km/jam x 3 jam).
Semakin lama waktu tempuh, semakin jauh jarak yang ditempuh. Begitu pula sebaliknya, jika waktu tempuh dipersingkat, maka jarak yang ditempuh juga akan berkurang. Hubungan ini menunjukkan perbandingan senilai yang jelas antara kecepatan (konstan), waktu tempuh, dan jarak tempuh.
Contoh Soal Perbandingan Senilai
Seorang pekerja dapat menyelesaikan 5 unit produk dalam 2 jam. Berapa unit produk yang dapat diselesaikan pekerja tersebut dalam 6 jam dengan kecepatan kerja yang sama?
- Tentukan perbandingan waktu: 6 jam / 2 jam = 3
- Kalikan jumlah produk dengan perbandingan waktu: 5 unit x 3 = 15 unit
- Kesimpulan: Pekerja tersebut dapat menyelesaikan 15 unit produk dalam 6 jam.
Karakteristik Perbandingan Senilai
Perbandingan senilai memiliki tiga karakteristik utama yang membedakannya dari perbandingan berbalik nilai. Ketiga karakteristik tersebut adalah:
- Jika satu besaran bertambah, besaran lainnya juga bertambah.
- Jika satu besaran berkurang, besaran lainnya juga berkurang.
- Hasil bagi antara kedua besaran selalu konstan.
Tabel Perbandingan Perbandingan Senilai dan Berbalik Nilai
| Nama Perbandingan | Rumus | Contoh |
|---|---|---|
| Perbandingan Senilai | a/b = k (konstanta) | Jumlah barang dan total harga |
| Perbandingan Berbalik Nilai | a x b = k (konstanta) | Kecepatan dan waktu tempuh (dengan jarak tetap) |
Cara Menyelesaikan Soal Perbandingan Senilai
Perbandingan senilai merupakan konsep matematika yang penting untuk memahami hubungan antara dua atau lebih besaran yang berubah secara proporsional. Memahami cara menyelesaikan soal perbandingan senilai sangat krusial dalam berbagai bidang, mulai dari ilmu pengetahuan hingga kehidupan sehari-hari. Berikut ini akan dijelaskan beberapa metode dan contoh soal untuk memperjelas pemahaman Anda.
Menyelesaikan Soal Perbandingan Senilai yang Melibatkan Tiga Besaran
Soal perbandingan senilai yang melibatkan tiga besaran dapat diselesaikan dengan menggunakan metode proporsi atau perbandingan langsung. Prinsip utamanya adalah menjaga kesetaraan rasio antar besaran. Dengan memahami hubungan proporsional antara ketiga besaran, kita dapat menemukan nilai yang belum diketahui.
Contoh: Tiga pekerja dapat menyelesaikan suatu pekerjaan dalam 6 hari. Berapa hari yang dibutuhkan oleh 2 pekerja untuk menyelesaikan pekerjaan yang sama?
Penyelesaian: Kita dapat membentuk perbandingan sebagai berikut: (Jumlah pekerja) x (Jumlah hari) = konstanta. Jadi, 3 pekerja x 6 hari = 18 pekerja-hari. Jika hanya ada 2 pekerja, maka jumlah hari yang dibutuhkan adalah 18 pekerja-hari / 2 pekerja = 9 hari.
Contoh Soal Cerita Perbandingan Senilai yang Kompleks dan Penyelesaiannya
Berikut contoh soal cerita yang lebih kompleks:
Sebuah mobil melaju dengan kecepatan 60 km/jam dan menempuh jarak 300 km dalam waktu tertentu. Jika kecepatan mobil ditingkatkan menjadi 75 km/jam, berapa jarak yang dapat ditempuh mobil dalam waktu yang sama?
Penyelesaian: Kita dapat menggunakan perbandingan senilai: Kecepatan x Waktu = Jarak. Waktu tetap sama pada kedua kasus. Jadi, kita punya perbandingan: (60 km/jam) x (Waktu) = 300 km dan (75 km/jam) x (Waktu) = Jarak baru. Dari persamaan pertama, kita dapat menemukan Waktu = 300 km / 60 km/jam = 5 jam. Substitusikan Waktu ke persamaan kedua: (75 km/jam) x 5 jam = 375 km.
Jadi, mobil dapat menempuh jarak 375 km dalam waktu yang sama.
Metode Proporsi dalam Menyelesaikan Soal Perbandingan Senilai
Metode proporsi merupakan cara yang sistematis untuk menyelesaikan soal perbandingan senilai. Metode ini melibatkan penyusunan perbandingan yang setara dan penyelesaian persamaan yang dihasilkan.
Contoh: Jika 5 kg beras harganya Rp 50.000, berapa harga 8 kg beras?
Penyelesaian: Kita dapat menyusun proporsi sebagai berikut: 5 kg / Rp 50.000 = 8 kg / x. Dengan menyelesaikan persamaan ini, kita dapatkan x = (8 kg x Rp 50.000) / 5 kg = Rp 80.000.
Contoh Soal Perbandingan Senilai yang Melibatkan Skala Peta dan Solusinya
Skala peta merupakan contoh aplikasi perbandingan senilai dalam kehidupan nyata. Skala peta menunjukkan perbandingan antara jarak pada peta dengan jarak sebenarnya di lapangan.
Contoh: Sebuah peta memiliki skala 1:100.000. Jika jarak antara dua kota pada peta adalah 5 cm, berapakah jarak sebenarnya antara kedua kota tersebut?
Penyelesaian: Skala 1:100.000 berarti 1 cm pada peta mewakili 100.000 cm di lapangan. Jadi, jarak sebenarnya adalah 5 cm x 100.000 = 500.000 cm = 5 km.
Langkah-langkah Menyelesaikan Soal Perbandingan Senilai dengan Metode Perbandingan
- Identifikasi besaran yang terlibat dan tentukan apakah mereka berbanding senilai atau berbanding terbalik.
- Buat perbandingan antara besaran-besaran tersebut.
- Susun persamaan berdasarkan perbandingan yang telah dibuat.
- Selesaikan persamaan untuk menemukan nilai yang belum diketahui.
- Tuliskan jawaban dengan satuan yang tepat.
Penerapan Perbandingan Senilai dalam Kehidupan Nyata: Contoh Perbandingan Senilai
Perbandingan senilai merupakan konsep matematika dasar yang memiliki aplikasi luas dalam berbagai aspek kehidupan. Kemampuan untuk memahami dan menerapkan perbandingan senilai memungkinkan kita untuk menyelesaikan masalah yang melibatkan proporsi, skala, dan hubungan kuantitatif antar variabel. Berikut beberapa contoh penerapan perbandingan senilai dalam kehidupan sehari-hari, khususnya dalam bidang ekonomi, pembangunan infrastruktur, penentuan harga, kesehatan, dan konstruksi.
Penerapan Perbandingan Senilai dalam Bidang Ekonomi
Perbandingan senilai sering digunakan dalam analisis ekonomi untuk memahami hubungan antara berbagai variabel ekonomi. Dengan memahami hubungan proporsional antar variabel, kita dapat memprediksi dampak perubahan pada satu variabel terhadap variabel lainnya.
- Permintaan dan Penawaran: Jika harga suatu barang naik, maka permintaan akan cenderung menurun, dan sebaliknya. Hubungan ini dapat dimodelkan menggunakan perbandingan senilai, membantu memprediksi jumlah barang yang akan terjual pada harga tertentu.
- Inflasi dan Daya Beli: Inflasi yang tinggi akan menurunkan daya beli masyarakat. Perbandingan senilai dapat digunakan untuk menghitung penurunan daya beli berdasarkan tingkat inflasi tertentu.
- Pendapatan dan Pengeluaran Konsumsi: Secara umum, peningkatan pendapatan akan diikuti dengan peningkatan pengeluaran konsumsi. Perbandingan senilai dapat digunakan untuk menganalisis hubungan ini dan memprediksi tingkat pengeluaran konsumsi berdasarkan pendapatan.
Perbandingan Senilai dalam Perencanaan Pembangunan Infrastruktur
Perencanaan pembangunan infrastruktur, seperti jalan raya atau jembatan, seringkali melibatkan perhitungan yang kompleks. Perbandingan senilai berperan penting dalam memastikan proporsi yang tepat dan efisiensi penggunaan sumber daya.
Contoh: Dalam pembangunan jalan raya, perbandingan senilai digunakan untuk menentukan jumlah material (aspal, semen, pasir, dll.) yang dibutuhkan berdasarkan panjang dan lebar jalan yang akan dibangun. Misalnya, jika untuk membangun 100 meter jalan dibutuhkan 10 ton aspal, maka untuk membangun 500 meter jalan dibutuhkan 50 ton aspal (dengan asumsi lebar dan spesifikasi jalan tetap sama).
Penentuan Harga Jual Produk Berdasarkan Biaya Produksi dan Keuntungan
Perbandingan senilai sangat krusial dalam menentukan harga jual produk yang menguntungkan. Harga jual harus mempertimbangkan biaya produksi dan target keuntungan.
Contoh: Jika biaya produksi suatu barang adalah Rp 10.000 dan target keuntungan adalah 20%, maka harga jual dapat dihitung dengan rumus: Harga Jual = Biaya Produksi / (1 – Margin Keuntungan). Dalam kasus ini, Harga Jual = Rp 10.000 / (1 – 0.20) = Rp 12.500.
Penerapan Perbandingan Senilai dalam Bidang Kesehatan: Perhitungan Dosis Obat
Dalam bidang kesehatan, perbandingan senilai sangat penting dalam menghitung dosis obat yang tepat untuk pasien. Dosis obat seringkali disesuaikan dengan berat badan atau usia pasien.
Contoh: Jika dosis obat untuk anak dengan berat badan 20 kg adalah 5 ml, maka dosis obat untuk anak dengan berat badan 30 kg dapat dihitung dengan perbandingan senilai: (30 kg / 20 kg) x 5 ml = 7,5 ml. (Perlu diingat bahwa ini hanya contoh ilustrasi dan dosis obat harus selalu ditentukan oleh tenaga medis profesional).
Penentuan Rasio Campuran Bahan Bangunan, Contoh perbandingan senilai
Perbandingan senilai juga berperan penting dalam menentukan rasio campuran bahan bangunan seperti semen, pasir, dan kerikil untuk membuat beton. Rasio yang tepat akan menghasilkan beton dengan kekuatan dan kualitas yang diinginkan.
Contoh: Rasio campuran beton standar seringkali menggunakan perbandingan 1:2:3 (semen:pasir:kerikil). Artinya, untuk setiap 1 sak semen, dibutuhkan 2 bagian pasir dan 3 bagian kerikil. Perbandingan ini dapat disesuaikan berdasarkan kebutuhan kekuatan dan jenis beton yang diinginkan.
Contoh Soal dan Pembahasan Perbandingan Senilai

Perbandingan senilai merupakan konsep matematika yang menjelaskan hubungan antara dua besaran yang berubah secara proporsional. Jika salah satu besaran meningkat, besaran lainnya juga meningkat dengan faktor pengali yang tetap. Memahami perbandingan senilai sangat penting dalam berbagai aplikasi, mulai dari menghitung skala peta hingga menyelesaikan permasalahan di bidang ekonomi dan fisika. Berikut beberapa contoh soal dan pembahasan untuk mengasah pemahaman kita.
Contoh Soal Perbandingan Senilai: Tingkat Kesulitan Mudah
Sebuah mobil melaju dengan kecepatan 60 km/jam dan menempuh jarak 120 km. Berapa waktu yang dibutuhkan mobil tersebut untuk menempuh jarak 180 km dengan kecepatan yang sama?
Pembahasan:
Kecepatan (v) = 60 km/jam
Jarak (s) = 120 km (awal) dan 180 km (tujuan)
Waktu (t) = s / v
Waktu untuk menempuh 120 km: t1 = 120 km / 60 km/jam = 2 jam
Karena kecepatan konstan, kita dapat menggunakan perbandingan senilai: s1/t1 = s2/t2
120 km / 2 jam = 180 km / t2
t2 = (180 km
– 2 jam) / 120 km = 3 jam
Jadi, waktu yang dibutuhkan untuk menempuh jarak 180 km adalah 3 jam.
Contoh Soal Perbandingan Senilai: Tingkat Kesulitan Sedang
Harga 5 kg beras adalah Rp 50.000. Berapa harga 8 kg beras dengan harga per kilogram yang sama?
Pembahasan:
Harga 5 kg beras = Rp 50.000
Harga 1 kg beras = Rp 50.000 / 5 kg = Rp 10.000/kg
Harga 8 kg beras = 8 kg
– Rp 10.000/kg = Rp 80.000
Atau dengan perbandingan senilai:
5 kg / Rp 50.000 = 8 kg / x
x = (8 kg
– Rp 50.000) / 5 kg = Rp 80.000
Jadi, harga 8 kg beras adalah Rp 80.000.
Contoh Soal Perbandingan Senilai: Tingkat Kesulitan Sulit
Sebuah proyek pembangunan gedung dapat diselesaikan oleh 15 pekerja dalam waktu 20 hari. Jika proyek tersebut ingin diselesaikan dalam waktu 15 hari, berapa banyak pekerja tambahan yang dibutuhkan?
Pembahasan:
Jumlah pekerja (P) berbanding terbalik dengan waktu (t) yang dibutuhkan. Artinya, semakin banyak pekerja, semakin sedikit waktu yang dibutuhkan. Kita dapat menggunakan rumus: P1
– t1 = P2
– t2
P1 = 15 pekerja
t1 = 20 hari
t2 = 15 hari
P2 = (P1
– t1) / t2 = (15 pekerja
– 20 hari) / 15 hari = 20 pekerja
Pekerja tambahan yang dibutuhkan = 20 pekerja – 15 pekerja = 5 pekerja
Jadi, dibutuhkan 5 pekerja tambahan.
Kesalahan umum yang sering terjadi dalam menyelesaikan soal perbandingan senilai adalah keliru dalam menentukan hubungan antara dua besaran. Seringkali, siswa salah mengidentifikasi apakah hubungan tersebut berbanding lurus atau berbanding terbalik. Perlu ketelitian dalam memahami konteks soal.
Ringkasan Rumus dan Contoh Soal
| Tingkat Kesulitan | Rumus | Contoh Soal | Jawaban |
|---|---|---|---|
| Mudah | a/b = c/d | Jika 2 apel harganya Rp 5.000, berapa harga 4 apel? | Rp 10.000 |
| Sedang | a/b = c/d | Sebuah mobil menempuh 100 km dalam 2 jam. Berapa kecepatan mobil tersebut? | 50 km/jam |
| Sulit | P1*t1 = P2*t2 | 20 orang menyelesaikan pekerjaan dalam 10 hari. Berapa hari yang dibutuhkan jika pekerja ditambah menjadi 25 orang? | 8 hari |
Contoh Soal Gabungan Perbandingan Senilai dan Berbalik Nilai
Sebuah pabrik memproduksi 1000 unit barang dalam 5 hari dengan 20 pekerja. Jika pabrik ingin memproduksi 1500 unit barang dalam 3 hari, berapa banyak pekerja tambahan yang dibutuhkan?
Pembahasan:
Pertama, kita perhatikan hubungan antara jumlah barang dan jumlah pekerja (perbandingan senilai): lebih banyak barang, lebih banyak pekerja.
Kemudian, kita perhatikan hubungan antara jumlah barang dan waktu (perbandingan senilai): lebih banyak barang, lebih banyak waktu.
Selanjutnya, kita perhatikan hubungan antara jumlah pekerja dan waktu (perbandingan berbalik nilai): lebih banyak pekerja, lebih sedikit waktu.
Kita bisa menggunakan rumus: (P1
– t1)/B1 = (P2
– t2)/B2
P1 = 20 pekerja
t1 = 5 hari
B1 = 1000 unit
t2 = 3 hari
B2 = 1500 unit
P2 = (P1
– t1
– B2) / (t2
– B1) = (20 pekerja
– 5 hari
– 1500 unit) / (3 hari
– 1000 unit) = 50 pekerja
Pekerja tambahan yang dibutuhkan = 50 pekerja – 20 pekerja = 30 pekerja
Jadi, dibutuhkan 30 pekerja tambahan.
Pemungkas
Memahami perbandingan senilai bukan hanya sekadar menguasai rumus matematika, tetapi juga tentang kemampuan berpikir logis dan analitis dalam memecahkan masalah. Setelah mempelajari berbagai contoh dan metode penyelesaian soal, diharapkan Anda dapat menerapkan konsep ini dalam berbagai situasi kehidupan nyata. Dengan latihan yang cukup, perbandingan senilai akan menjadi alat yang ampuh untuk menyelesaikan berbagai permasalahan yang melibatkan hubungan antara besaran-besaran yang saling bergantung.