- Pengertian Regresi Sederhana
- Asumsi Regresi Sederhana
-
Metode Perhitungan Regresi Sederhana
- Langkah-langkah Perhitungan Regresi Sederhana Secara Manual, Analisis regresi sederhana
- Rumus-Rumus yang Digunakan dalam Perhitungan Regresi Sederhana
- Contoh Perhitungan Regresi Sederhana dengan Data Numerik
- Perbandingan Perhitungan Manual dengan Penggunaan Software Statistik
- Interpretasi Koefisien Regresi dan Konstanta
- Interpretasi Hasil Regresi Sederhana
- Penerapan Regresi Sederhana dalam Studi Kasus: Analisis Regresi Sederhana
- Kesimpulan Akhir
Analisis regresi sederhana merupakan alat statistik yang ampuh untuk mengungkap hubungan antara dua variabel. Bayangkan Anda ingin memprediksi harga rumah berdasarkan luas tanahnya; regresi sederhana dapat membantu! Metode ini membantu kita memahami bagaimana perubahan pada satu variabel (independen) memengaruhi variabel lainnya (dependen), memberikan wawasan berharga dalam berbagai bidang, mulai dari ekonomi hingga ilmu kesehatan.
Dalam pembahasan ini, kita akan menjelajahi pengertian regresi sederhana, asumsi-asumsinya, metode perhitungan, interpretasi hasil, dan penerapannya dalam studi kasus. Dengan pemahaman yang komprehensif, Anda akan mampu memanfaatkan teknik ini untuk menganalisis data dan mengambil keputusan yang lebih tepat.
Pengertian Regresi Sederhana
Analisis regresi sederhana merupakan metode statistik yang digunakan untuk memodelkan hubungan antara satu variabel dependen (terikat) dan satu variabel independen (bebas). Metode ini bertujuan untuk mengestimasi bagaimana perubahan pada variabel independen akan memengaruhi variabel dependen. Dengan kata lain, regresi sederhana membantu kita memahami dan memprediksi nilai variabel dependen berdasarkan nilai variabel independen.
Contoh Penerapan Regresi Sederhana
Salah satu contoh penerapan regresi sederhana adalah dalam memprediksi harga rumah berdasarkan luas bangunan. Dalam kasus ini, luas bangunan (variabel independen) diasumsikan memengaruhi harga rumah (variabel dependen). Semakin luas bangunan, maka harga rumah cenderung semakin tinggi. Contoh lain adalah memprediksi nilai ujian siswa berdasarkan jumlah jam belajar. Semakin banyak jam belajar, maka nilai ujian siswa diharapkan semakin tinggi.
Tentu saja, ini merupakan model sederhana dan faktor lain juga dapat memengaruhi harga rumah dan nilai ujian.
Variabel Dependen dan Independen
Dalam analisis regresi sederhana, identifikasi variabel dependen dan independen sangat penting. Variabel dependen adalah variabel yang nilainya dipengaruhi oleh variabel independen. Variabel independen adalah variabel yang nilainya diasumsikan memengaruhi variabel dependen. Kembali ke contoh sebelumnya, harga rumah adalah variabel dependen, sementara luas bangunan adalah variabel independen. Begitu pula, nilai ujian adalah variabel dependen, sedangkan jumlah jam belajar adalah variabel independen.
Perbandingan Regresi Sederhana dengan Metode Statistik Lainnya
Berikut perbandingan regresi sederhana dengan beberapa metode statistik lainnya:
| Metode | Deskripsi Singkat | Kegunaan | Kelemahan |
|---|---|---|---|
| Regresi Sederhana | Memmodelkan hubungan linier antara satu variabel dependen dan satu variabel independen. | Memprediksi nilai variabel dependen berdasarkan nilai variabel independen; menguji signifikansi hubungan antara kedua variabel. | Hanya dapat menganalisis hubungan linier; asumsi-asumsi yang ketat harus dipenuhi; tidak memperhitungkan variabel lain yang mungkin memengaruhi variabel dependen. |
| Regresi Berganda | Memmodelkan hubungan linier antara satu variabel dependen dan dua atau lebih variabel independen. | Memprediksi nilai variabel dependen dengan mempertimbangkan beberapa variabel independen; menguji signifikansi pengaruh masing-masing variabel independen. | Lebih kompleks daripada regresi sederhana; asumsi-asumsi yang ketat harus dipenuhi; interpretasi hasil dapat menjadi lebih rumit. |
| Korelasi | Mengukur kekuatan dan arah hubungan antara dua variabel. | Menentukan seberapa kuat hubungan antara dua variabel; tidak digunakan untuk prediksi. | Hanya mengukur hubungan, tidak menjelaskan sebab akibat; rentan terhadap outlier. |
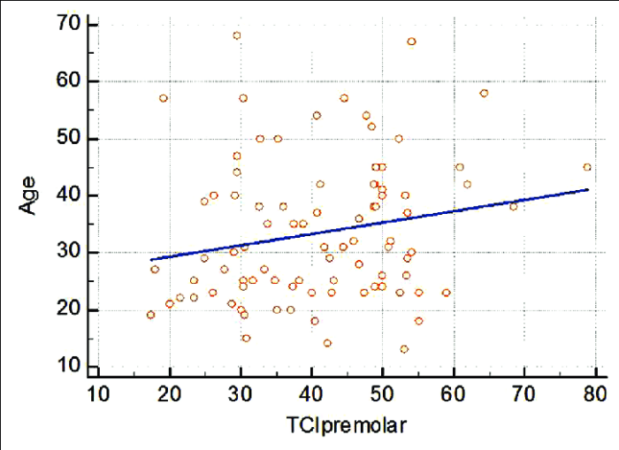
Ilustrasi Grafik Hubungan Variabel Dependen dan Independen
Hubungan antara variabel dependen dan independen dalam regresi sederhana dapat digambarkan dengan grafik scatter plot. Pada sumbu X, kita tempatkan variabel independen, dan pada sumbu Y, kita tempatkan variabel dependen. Setiap titik pada grafik mewakili satu observasi (misalnya, satu rumah dengan luas bangunan tertentu dan harga tertentu). Garis regresi, yang merupakan garis lurus terbaik yang sesuai dengan titik-titik data, menggambarkan hubungan linier antara kedua variabel.
Kemiringan garis menunjukkan kekuatan dan arah hubungan. Kemiringan positif menunjukkan hubungan positif (semakin besar variabel independen, semakin besar variabel dependen), sedangkan kemiringan negatif menunjukkan hubungan negatif (semakin besar variabel independen, semakin kecil variabel dependen). Jika titik-titik data tersebar jauh dari garis regresi, hal ini menunjukkan bahwa model regresi sederhana mungkin tidak sesuai dengan data.
Asumsi Regresi Sederhana
Analisis regresi sederhana, meskipun tampak sederhana, bergantung pada beberapa asumsi kunci agar hasil analisisnya valid dan dapat diinterpretasi dengan benar. Pelanggaran terhadap asumsi-asumsi ini dapat menyebabkan bias dalam estimasi parameter dan kesimpulan yang salah. Oleh karena itu, penting untuk memahami dan memeriksa asumsi-asumsi ini sebelum melakukan interpretasi hasil regresi.
Linearitas Hubungan
Asumsi linearitas menyatakan bahwa hubungan antara variabel dependen (Y) dan variabel independen (X) bersifat linear. Artinya, perubahan pada X akan menyebabkan perubahan pada Y yang proporsional dan konsisten. Jika hubungannya non-linear, model regresi sederhana mungkin tidak mampu menangkap pola hubungan yang sebenarnya. Hal ini dapat mengakibatkan prediksi yang tidak akurat.
Untuk memeriksa asumsi ini, kita dapat membuat scatter plot antara variabel Y dan X. Jika titik-titik data membentuk pola garis lurus, maka asumsi linearitas terpenuhi. Jika pola titik-titik data membentuk kurva, maka asumsi linearitas terlanggar. Transformasi data, seperti logaritma atau kuadrat, dapat digunakan untuk meluruskan hubungan non-linear.
Independensi Observasi
Asumsi independensi menyatakan bahwa observasi satu dengan yang lain tidak saling berkorelasi. Pelanggaran asumsi ini sering terjadi pada data time series atau data panel, di mana observasi yang berdekatan cenderung saling mempengaruhi. Jika observasi tidak independen, estimasi standar error akan bias, sehingga uji signifikansi parameter menjadi tidak valid.
Pengujian terhadap asumsi ini bisa dilakukan dengan melihat korelasi antar residual. Nilai korelasi yang signifikan mengindikasikan pelanggaran asumsi independensi. Salah satu cara mengatasi pelanggaran asumsi ini adalah dengan menggunakan model regresi yang memperhitungkan korelasi antar observasi, seperti model regresi autoregresif (AR) atau model regresi moving average (MA).
Homoskedastisitas
Asumsi homoskedastisitas menyatakan bahwa variansi dari residual konstan untuk semua nilai X. Pelanggaran asumsi ini, yang disebut heteroskedastisitas, terjadi ketika variansi residual berubah-ubah seiring perubahan nilai X. Heteroskedastisitas menyebabkan estimasi standar error menjadi tidak efisien, sehingga uji signifikansi parameter menjadi tidak akurat.
Untuk memeriksa homoskedastisitas, kita dapat membuat scatter plot antara residual dan nilai prediksi (Y topi). Jika variansi residual konstan, maka titik-titik data akan tersebar secara merata di sekitar garis horizontal nol. Jika variansi residual berubah-ubah, maka titik-titik data akan membentuk pola kerucut atau pola lainnya yang menunjukkan adanya heteroskedastisitas. Salah satu cara mengatasi heteroskedastisitas adalah dengan melakukan transformasi data atau menggunakan metode weighted least squares (WLS).
Normalitas Residual
Asumsi normalitas menyatakan bahwa residual terdistribusi normal dengan rata-rata nol. Asumsi ini penting untuk uji signifikansi parameter dan interval kepercayaan. Jika residual tidak terdistribusi normal, uji signifikansi parameter mungkin tidak valid.
Normalitas residual dapat diperiksa dengan menggunakan histogram, Q-Q plot, atau uji statistik seperti uji Shapiro-Wilk. Jika residual tidak terdistribusi normal, transformasi data atau penggunaan metode non-parametrik dapat dipertimbangkan.
Tidak adanya Multikolinearitas
Meskipun ini adalah regresi sederhana (hanya satu variabel independen), penting untuk memastikan tidak adanya multikolinearitas. Dalam konteks regresi sederhana, ini kurang relevan, tetapi penting untuk diingat saat memperluas ke regresi berganda. Multikolinearitas terjadi ketika variabel independen saling berkorelasi tinggi. Dalam regresi sederhana, hal ini tidak mungkin terjadi karena hanya ada satu variabel independen. Namun, pemahaman ini penting untuk transisi ke model regresi yang lebih kompleks.
Cara Mengatasi Pelanggaran Asumsi Regresi Sederhana
- Transformasi data (logaritma, akar kuadrat, dll.)
- Penggunaan model regresi yang berbeda (misalnya, model non-parametrik)
- Penggunaan metode weighted least squares (WLS)
- Penggunaan model regresi yang memperhitungkan korelasi antar observasi (misalnya, model ARIMA)
Memenuhi asumsi regresi sederhana sangat penting untuk mendapatkan hasil yang valid dan dapat diandalkan. Pelanggaran asumsi dapat menyebabkan bias dalam estimasi parameter, interval kepercayaan yang tidak akurat, dan kesimpulan yang salah. Oleh karena itu, pemeriksaan asumsi merupakan langkah krusial dalam analisis regresi.
Metode Perhitungan Regresi Sederhana
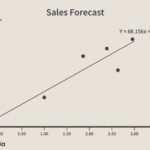
Regresi sederhana merupakan teknik statistik yang digunakan untuk memodelkan hubungan linier antara dua variabel. Pemahaman tentang metode perhitungannya sangat penting untuk dapat menginterpretasi hasil analisis dan mengambil kesimpulan yang tepat. Berikut ini akan diuraikan langkah-langkah perhitungan regresi sederhana secara manual, disertai contoh dan perbandingan dengan penggunaan software statistik.
Langkah-langkah Perhitungan Regresi Sederhana Secara Manual, Analisis regresi sederhana
Perhitungan regresi sederhana secara manual melibatkan beberapa tahapan, dimulai dari perhitungan nilai rata-rata hingga penentuan persamaan garis regresi. Ketelitian dalam setiap langkah sangat krusial untuk mendapatkan hasil yang akurat.
- Hitung rata-rata variabel X (variabel independen) dan Y (variabel dependen).
- Hitung deviasi setiap nilai X dan Y dari rata-ratanya (X – X̄ dan Y – Ȳ).
- Hitung perkalian deviasi X dan Y untuk setiap pasangan data: (X – X̄)(Y – Ȳ).
- Hitung kuadrat deviasi X: (X – X̄)2.
- Hitung koefisien regresi b (kemiringan garis regresi) menggunakan rumus:
b = Σ[(X - X̄)(Y - Ȳ)] / Σ[(X - X̄)2] - Hitung konstanta a (intercept) menggunakan rumus:
a = Ȳ - bX̄ - Tentukan persamaan garis regresi:
Y = a + bX
Rumus-Rumus yang Digunakan dalam Perhitungan Regresi Sederhana
Rumus-rumus yang digunakan di atas merupakan inti dari perhitungan regresi sederhana. Pemahaman terhadap rumus-rumus ini akan memudahkan dalam memahami proses dan interpretasi hasil.
b = Σ[(X - X̄)(Y - Ȳ)] / Σ[(X - X̄)2]: Rumus untuk menghitung koefisien regresi (kemiringan garis regresi).a = Ȳ: Rumus untuk menghitung konstanta (intercept) dari garis regresi.
-bX̄Y = a + bX: Persamaan garis regresi yang menunjukkan hubungan antara variabel X dan Y.
Contoh Perhitungan Regresi Sederhana dengan Data Numerik
Misalnya, kita ingin mengetahui hubungan antara jumlah jam belajar (X) dan nilai ujian (Y) dari 5 mahasiswa. Data sebagai berikut:
| Mahasiswa | Jam Belajar (X) | Nilai Ujian (Y) |
|---|---|---|
| 1 | 2 | 60 |
| 2 | 4 | 70 |
| 3 | 6 | 80 |
| 4 | 8 | 90 |
| 5 | 10 | 100 |
Dengan mengikuti langkah-langkah di atas, kita akan mendapatkan nilai X̄ = 6, Ȳ = 80, b = 10, dan a = 20. Oleh karena itu, persamaan garis regresinya adalah Y = 20 + 10X.
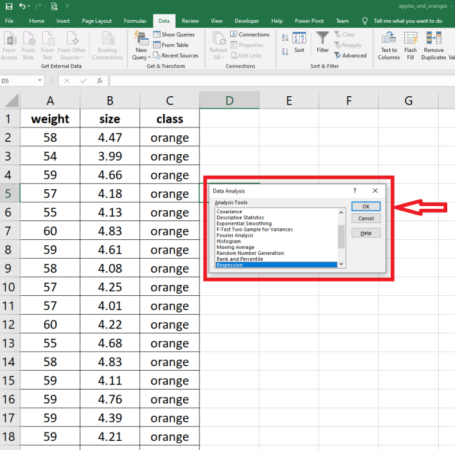
Perbandingan Perhitungan Manual dengan Penggunaan Software Statistik
Perhitungan manual cocok untuk data dengan jumlah observasi yang sedikit. Namun, untuk data dengan jumlah observasi yang besar, penggunaan software statistik seperti SPSS, R, atau Excel akan jauh lebih efisien dan mengurangi kemungkinan kesalahan perhitungan. Software statistik ini akan otomatis menghitung koefisien regresi, konstanta, dan memberikan berbagai informasi statistik lainnya seperti nilai R-squared.
Interpretasi Koefisien Regresi dan Konstanta
Dalam contoh di atas, koefisien regresi (b = 10) menunjukkan bahwa setiap penambahan 1 jam belajar akan meningkatkan nilai ujian sebesar 10 poin. Konstanta (a = 20) menunjukkan nilai ujian yang diperkirakan jika jumlah jam belajar adalah 0. Interpretasi ini perlu mempertimbangkan konteks data dan asumsi-asumsi yang mendasari analisis regresi.
Interpretasi Hasil Regresi Sederhana
Setelah melakukan analisis regresi sederhana, langkah selanjutnya adalah menginterpretasi hasil yang diperoleh. Interpretasi yang tepat akan memberikan pemahaman yang mendalam tentang hubungan antara variabel dependen dan independen. Proses ini melibatkan pemahaman nilai R-squared, koefisien regresi, dan uji signifikansi.
Nilai R-squared
R-squared (R²) merupakan ukuran yang menunjukkan seberapa baik model regresi menjelaskan variansi dalam variabel dependen. Nilai R² berkisar antara 0 hingga 1. Semakin mendekati 1, semakin baik model dalam menjelaskan variansi data. Misalnya, nilai R² sebesar 0,85 menunjukkan bahwa 85% variansi dalam variabel dependen dapat dijelaskan oleh variabel independen dalam model. Namun, perlu diingat bahwa R² yang tinggi tidak selalu menjamin model yang baik, karena bisa jadi terjadi overfitting.
Interpretasi Koefisien Regresi
Koefisien regresi menunjukkan pengaruh variabel independen terhadap variabel dependen. Misalnya, dalam model regresi yang memprediksi harga rumah (variabel dependen) berdasarkan luas tanah (variabel independen), koefisien regresi menunjukkan seberapa besar perubahan harga rumah untuk setiap peningkatan satu unit luas tanah. Jika koefisien regresi bernilai positif, maka peningkatan variabel independen akan diiringi peningkatan variabel dependen. Sebaliknya, jika bernilai negatif, peningkatan variabel independen akan menurunkan variabel dependen.
Sebagai contoh, jika koefisien regresi adalah 1000, artinya setiap penambahan 1 meter persegi luas tanah akan meningkatkan harga rumah sebesar Rp 1.000.000.
Uji Signifikansi Koefisien Regresi
Uji signifikansi koefisien regresi digunakan untuk menguji apakah hubungan antara variabel independen dan dependen signifikan secara statistik. Uji ini biasanya menggunakan p-value. Jika p-value kurang dari tingkat signifikansi yang telah ditentukan (misalnya, 0,05), maka hubungan tersebut signifikan secara statistik. Artinya, kecil kemungkinan hubungan yang diamati terjadi secara kebetulan. Sebaliknya, jika p-value lebih besar dari tingkat signifikansi, maka hubungan tersebut tidak signifikan secara statistik.
Tabel Ringkasan Interpretasi Output Regresi Sederhana
| Output | Nilai | Interpretasi | Implikasi |
|---|---|---|---|
| Koefisien Regresi (b) | 1000 | Peningkatan 1 m² luas tanah meningkatkan harga rumah sebesar Rp 1.000.000 | Luas tanah berpengaruh positif terhadap harga rumah |
| P-value (b) | 0.001 | Hubungan antara luas tanah dan harga rumah signifikan secara statistik (α = 0.05) | Model dapat diandalkan untuk memprediksi harga rumah berdasarkan luas tanah |
| R-squared (R²) | 0.75 | 75% variansi harga rumah dijelaskan oleh luas tanah | Model cukup baik dalam menjelaskan variansi harga rumah |
Batasan Interpretasi Hasil Regresi Sederhana
Regresi sederhana mengasumsikan hubungan linear antara variabel dependen dan independen. Hasil regresi hanya menunjukkan hubungan, bukan sebab-akibat. Faktor lain yang tidak dimasukkan dalam model dapat memengaruhi variabel dependen. Interpretasi harus mempertimbangkan konteks data dan batasan metode.
Penerapan Regresi Sederhana dalam Studi Kasus: Analisis Regresi Sederhana
Analisis regresi sederhana merupakan alat statistik yang ampuh untuk mengkaji hubungan antara dua variabel. Dengan memahami prinsip kerjanya, kita dapat mengaplikasikannya pada berbagai studi kasus untuk menemukan pola dan membuat prediksi. Berikut ini akan dijelaskan penerapan regresi sederhana melalui sebuah contoh studi kasus, mulai dari penentuan variabel hingga interpretasi hasil.
Studi Kasus: Hubungan antara Jam Belajar dan Nilai Ujian
Studi kasus ini akan meneliti hubungan antara jumlah jam belajar (variabel independen) dan nilai ujian statistik (variabel dependen) dari sekelompok mahasiswa. Diasumsikan bahwa semakin banyak jam belajar, maka nilai ujian akan semakin tinggi. Hipotesis ini akan diuji menggunakan analisis regresi sederhana.
Variabel Dependen dan Independen
Dalam studi kasus ini, variabel dependen adalah nilai ujian statistik. Variabel ini merupakan variabel yang dipengaruhi oleh variabel lain. Sementara itu, variabel independen adalah jumlah jam belajar, yaitu variabel yang diasumsikan mempengaruhi nilai ujian statistik.
Langkah-Langkah Analisis Regresi Sederhana
Analisis regresi sederhana pada studi kasus ini melibatkan beberapa langkah. Pertama, data jumlah jam belajar dan nilai ujian dari sejumlah mahasiswa dikumpulkan. Kemudian, data tersebut diolah menggunakan software statistik seperti SPSS atau R untuk menghasilkan persamaan regresi linier. Persamaan ini akan berbentuk Y = a + bX, di mana Y adalah nilai ujian, X adalah jumlah jam belajar, a adalah konstanta, dan b adalah koefisien regresi.
Koefisien regresi (b) menunjukkan pengaruh perubahan satu unit variabel independen (jam belajar) terhadap variabel dependen (nilai ujian). Langkah selanjutnya adalah menguji signifikansi model regresi dan koefisien regresi menggunakan uji t dan uji F. Uji ini akan menentukan apakah hubungan antara variabel independen dan dependen signifikan secara statistik.
Hasil Analisis dan Interpretasi
Misalkan setelah dilakukan analisis regresi sederhana, diperoleh persamaan regresi Y = 50 + 5X. Ini berarti bahwa untuk setiap penambahan satu jam belajar, nilai ujian diperkirakan akan meningkat sebesar 5 poin, dengan nilai dasar 50 poin jika tidak belajar sama sekali. Nilai R-squared (koefisien determinasi) menunjukkan proporsi variansi dalam variabel dependen yang dijelaskan oleh variabel independen. Misalnya, jika R-squared = 0.7, maka 70% variansi nilai ujian dapat dijelaskan oleh jumlah jam belajar.
Uji signifikansi (uji t dan uji F) akan menunjukkan apakah koefisien regresi dan model regresi secara keseluruhan signifikan secara statistik. Hasil uji signifikansi biasanya ditunjukkan oleh nilai p-value. Jika p-value kurang dari 0.05, maka hubungan antara variabel independen dan dependen dianggap signifikan secara statistik.
Keterbatasan dan Implikasi Hasil Analisis
Meskipun analisis regresi sederhana memberikan informasi berharga tentang hubungan antara jam belajar dan nilai ujian, terdapat beberapa keterbatasan. Model ini hanya mempertimbangkan satu variabel independen, padahal faktor lain seperti kualitas metode belajar, kemampuan bawaan, dan kondisi kesehatan juga dapat mempengaruhi nilai ujian. Oleh karena itu, hasil analisis ini hanya memberikan gambaran parsial dari faktor-faktor yang mempengaruhi nilai ujian.
Implikasinya, hasil analisis ini tidak dapat digunakan untuk membuat kesimpulan kausalitas secara pasti. Peningkatan nilai ujian tidak sepenuhnya disebabkan oleh peningkatan jam belajar saja. Hasil ini lebih tepat diinterpretasikan sebagai korelasi, bukan kausalitas. Studi lebih lanjut dengan mempertimbangkan variabel lain diperlukan untuk mendapatkan pemahaman yang lebih komprehensif.
Kesimpulan Akhir
Analisis regresi sederhana, meskipun sederhana dalam namanya, menawarkan kekuatan besar dalam mengungkap hubungan antara variabel. Dengan memahami asumsi-asumsinya, melakukan perhitungan yang tepat, dan menginterpretasi hasil dengan hati-hati, kita dapat memperoleh wawasan berharga dari data. Ingatlah bahwa keterbatasan metode ini perlu dipertimbangkan, dan hasil analisis harus diinterpretasikan dalam konteks permasalahan yang dihadapi.