Analisis regresi berganda merupakan teknik statistik yang ampuh untuk mengungkap hubungan antara satu variabel dependen dengan dua atau lebih variabel independen. Bayangkan Anda ingin memprediksi harga rumah; bukan hanya luas tanah yang berpengaruh, tetapi juga lokasi, jumlah kamar tidur, dan fasilitas lainnya. Regresi berganda memungkinkan kita untuk mempertimbangkan semua faktor tersebut secara simultan, memberikan prediksi yang lebih akurat dan komprehensif dibandingkan dengan analisis regresi linear sederhana.
Dalam uraian berikut, kita akan menjelajahi konsep dasar regresi berganda, mulai dari model matematikanya hingga interpretasi hasil analisis. Kita akan membahas metode estimasi parameter, pengujian hipotesis, dan bagaimana mengaplikasikannya dalam berbagai konteks. Dengan pemahaman yang mendalam tentang regresi berganda, Anda dapat menganalisis data dengan lebih efektif dan mengambil keputusan yang lebih tepat berdasarkan bukti empiris.
Pengertian Regresi Berganda
Analisis regresi berganda merupakan teknik statistik yang digunakan untuk memodelkan hubungan antara satu variabel dependen (terikat) dengan dua atau lebih variabel independen (bebas). Berbeda dengan regresi linear sederhana yang hanya melibatkan satu variabel independen, regresi berganda memungkinkan kita untuk menganalisis pengaruh beberapa faktor secara simultan terhadap variabel yang kita teliti. Kemampuan ini memberikan pemahaman yang lebih komprehensif dan akurat mengenai faktor-faktor yang berperan dalam menentukan nilai variabel dependen.
Konsep Regresi Berganda
Regresi berganda bertujuan untuk menemukan persamaan matematis yang terbaik yang menggambarkan hubungan antara variabel dependen dan variabel independen. Persamaan ini memungkinkan kita untuk memprediksi nilai variabel dependen berdasarkan nilai-nilai variabel independen yang diketahui. Proses ini melibatkan estimasi parameter-parameter dalam persamaan, yang merepresentasikan pengaruh masing-masing variabel independen terhadap variabel dependen. Penggunaan metode kuadrat terkecil (OLS) merupakan metode umum dalam estimasi parameter ini, meminimalkan jumlah kuadrat dari selisih antara nilai sebenarnya dan nilai yang diprediksi dari variabel dependen.
Contoh Penerapan Regresi Berganda
Sebagai contoh, sebuah perusahaan ritel mungkin ingin memprediksi penjualan (variabel dependen) berdasarkan faktor-faktor seperti biaya iklan, harga produk, dan lokasi toko (variabel independen). Dengan menggunakan regresi berganda, perusahaan dapat menganalisis kontribusi relatif dari masing-masing faktor terhadap penjualan dan mengoptimalkan strategi pemasarannya. Contoh lain adalah dalam bidang kesehatan, dimana regresi berganda dapat digunakan untuk memprediksi risiko penyakit jantung berdasarkan faktor-faktor seperti tekanan darah, kolesterol, dan kebiasaan merokok.
Perbandingan Regresi Berganda dan Regresi Linear Sederhana
Perbedaan utama antara regresi berganda dan regresi linear sederhana terletak pada jumlah variabel independen yang digunakan. Regresi linear sederhana hanya melibatkan satu variabel independen, sedangkan regresi berganda melibatkan dua atau lebih. Hal ini memberikan regresi berganda kemampuan yang lebih besar dalam menjelaskan variabilitas variabel dependen dan menghasilkan prediksi yang lebih akurat, meskipun kompleksitas model juga meningkat.
Asumsi-Asumsi Dasar Analisis Regresi Berganda
Penerapan analisis regresi berganda didasarkan pada beberapa asumsi dasar yang perlu dipenuhi agar hasil analisis dapat diandalkan. Penting untuk memeriksa asumsi-asumsi ini sebelum menginterpretasikan hasil analisis. Kegagalan untuk memenuhi asumsi-asumsi ini dapat menyebabkan hasil yang bias dan tidak akurat.
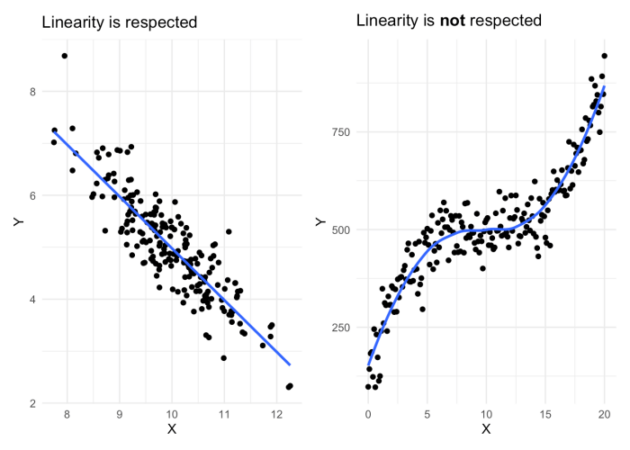
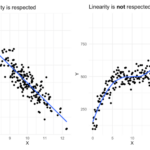
- Linearitas: Hubungan antara variabel dependen dan independen bersifat linear.
- Independensi: Pengamatan saling independen satu sama lain.
- Homoskedastisitas: Varians residual konstan untuk semua nilai variabel independen.
- Normalitas: Residual terdistribusi normal.
- Tidak adanya multikolinearitas: Tidak ada korelasi yang tinggi antar variabel independen.
Karakteristik Perbandingan Regresi Berganda dan Regresi Linear Sederhana
| Jenis Regresi | Jumlah Variabel Independen | Rumus Dasar | Kegunaan |
|---|---|---|---|
| Regresi Linear Sederhana | Satu |
|
Menganalisis hubungan antara satu variabel dependen dan satu variabel independen. |
| Regresi Berganda | Dua atau lebih |
|
Menganalisis hubungan antara satu variabel dependen dan dua atau lebih variabel independen. |
Model Matematika Regresi Berganda
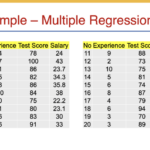
Analisis regresi berganda digunakan untuk memodelkan hubungan antara satu variabel dependen (terikat) dan dua atau lebih variabel independen (bebas). Model ini memungkinkan kita untuk memprediksi nilai variabel dependen berdasarkan nilai variabel independen yang diketahui. Pemahaman yang baik tentang model matematika regresi berganda sangat krusial untuk interpretasi hasil analisis.
Berikut ini akan dijelaskan rumus umum, interpretasi koefisien, dan contoh perhitungan manual regresi berganda.
Rumus Umum Regresi Berganda, Analisis regresi berganda
Rumus umum model regresi berganda linear dapat ditulis sebagai berikut:
Y = β0 + β 1X 1 + β 2X 2 + … + β kX k + ε
di mana:
- Y adalah variabel dependen (variabel yang diprediksi).
- X 1, X 2, …, X k adalah variabel independen (variabel prediktor).
- β 0 adalah konstanta (intercept), nilai Y ketika semua X bernilai nol.
- β 1, β 2, …, β k adalah koefisien regresi, menunjukkan pengaruh masing-masing variabel independen terhadap variabel dependen. Nilai ini mengindikasikan perubahan rata-rata Y untuk setiap perubahan satu satuan X, dengan asumsi variabel independen lainnya konstan.
- ε adalah error term (galat), mewakili variasi yang tidak dapat dijelaskan oleh model.
Contoh Rumus Regresi Berganda dengan Tiga Variabel Independen
Misalnya, kita ingin memprediksi harga rumah (Y) berdasarkan luas tanah (X 1), jumlah kamar tidur (X 2), dan lokasi (X 3). Model regresi berganda-nya dapat ditulis sebagai:
Y = β0 + β 1X 1 + β 2X 2 + β 3X 3 + ε
Interpretasi Koefisien Regresi
Koefisien regresi (β i) menunjukkan besarnya pengaruh setiap variabel independen terhadap variabel dependen. Misalnya, jika β 1 = 1000, ini berarti bahwa setiap penambahan satu unit luas tanah (misalnya, satu meter persegi) akan meningkatkan harga rumah rata-rata sebesar 1000 rupiah, dengan asumsi jumlah kamar tidur dan lokasi tetap sama. Tanda koefisien (positif atau negatif) menunjukkan arah hubungan. Koefisien positif menunjukkan hubungan positif (semakin besar X, semakin besar Y), sedangkan koefisien negatif menunjukkan hubungan negatif (semakin besar X, semakin kecil Y).
Contoh Perhitungan Manual Regresi Berganda Sederhana (Dua Variabel Independen)
Berikut ini contoh perhitungan manual regresi berganda sederhana dengan dua variabel independen. Perhitungan ini memerlukan penggunaan metode matriks atau software statistik, namun langkah-langkah dasar dapat diilustrasikan sebagai berikut:
Misalkan kita memiliki data penjualan (Y) yang dipengaruhi oleh biaya iklan (X1) dan harga produk (X 2). Data tersebut dapat direpresentasikan dalam bentuk matriks dan kemudian dilakukan perhitungan untuk memperoleh nilai β 0, β 1, dan β 2. Perhitungan ini melibatkan penyelesaian persamaan normal atau metode kuadrat terkecil (Ordinary Least Square/OLS). Prosesnya cukup kompleks dan membutuhkan pemahaman aljabar linear dan statistika yang mendalam. Software statistik seperti R, SPSS, atau Excel dapat mempermudah perhitungan ini.
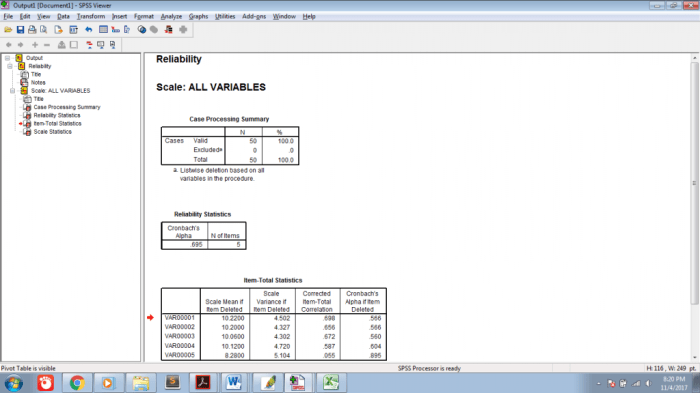
Sebagai contoh ilustrasi, bayangkan kita memiliki 5 data penjualan (Y), biaya iklan (X1), dan harga produk (X2). Setelah memasukkan data ke dalam software statistik, kita akan mendapatkan output yang berisi nilai β0, β1, dan β2, serta statistik lain seperti R-squared. Nilai-nilai ini kemudian dapat digunakan untuk membangun model regresi dan memprediksi penjualan berdasarkan biaya iklan dan harga produk.
Metode Estimasi Parameter
Estimasi parameter merupakan langkah krusial dalam analisis regresi berganda. Tujuannya adalah untuk menemukan nilai-nilai koefisien regresi yang paling tepat menggambarkan hubungan antara variabel dependen dan variabel independen. Metode yang paling umum digunakan adalah metode kuadrat terkecil (Ordinary Least Squares/OLS). Metode ini akan dijelaskan secara detail berikut ini, termasuk perbandingannya dengan metode lain (jika ada) dan ilustrasi perhitungannya dengan data hipotetis.
Metode Kuadrat Terkecil (OLS) dalam Regresi Berganda
Metode Kuadrat Terkecil (OLS) bertujuan meminimalkan jumlah kuadrat sisa (residual sum of squares/RSS), yaitu selisih kuadrat antara nilai aktual variabel dependen dan nilai yang diprediksi oleh model regresi. Dalam konteks regresi berganda, OLS mencari koefisien regresi yang menghasilkan garis regresi yang paling “dekat” dengan seluruh titik data. Kedekatan ini diukur melalui minimisasi RSS. Semakin kecil RSS, semakin baik model regresi tersebut dalam menjelaskan data.
Langkah-langkah Perhitungan OLS
Perhitungan OLS melibatkan beberapa langkah matematis yang umumnya dilakukan dengan bantuan perangkat lunak statistik. Namun, memahami langkah-langkah dasarnya penting untuk interpretasi hasil. Berikut uraiannya:
- Menentukan Model Regresi: Tentukan model regresi yang akan digunakan, misalnya Y = β 0 + β 1X 1 + β 2X 2 + ε, di mana Y adalah variabel dependen, X 1 dan X 2 adalah variabel independen, β 0 adalah konstanta, β 1 dan β 2 adalah koefisien regresi, dan ε adalah error term.
- Mengumpulkan Data: Kumpulkan data untuk variabel dependen dan independen.
- Menghitung Matriks X’X dan X’Y: Matriks X’X adalah matriks perkalian transpos matriks X (matriks variabel independen, termasuk kolom konstanta) dengan matriks X sendiri. Matriks X’Y adalah perkalian transpos matriks X dengan vektor Y (vektor variabel dependen).
- Menghitung Invers Matriks X’X: Hitung invers dari matriks X’X. Invers ini diperlukan untuk menghitung koefisien regresi.
- Menghitung Koefisien Regresi: Koefisien regresi (β) dihitung dengan rumus: β = (X’X) -1X’Y. Hasil perhitungan ini akan menghasilkan nilai β 0, β 1, dan β 2.
Perbandingan OLS dengan Metode Estimasi Lain
Meskipun OLS merupakan metode yang paling umum digunakan, terdapat metode estimasi parameter lain, seperti Maximum Likelihood Estimation (MLE). OLS relatif mudah dihitung dan diinterpretasikan, dan memiliki sifat-sifat statistik yang baik dalam kondisi tertentu. Namun, OLS memiliki asumsi-asumsi yang perlu dipenuhi. Jika asumsi-asumsi tersebut dilanggar (misalnya, adanya heteroskedastisitas atau autokorelasi), maka metode estimasi lain mungkin lebih tepat digunakan.
MLE, misalnya, lebih fleksibel dalam menangani distribusi error yang tidak normal.
Ilustrasi Perhitungan OLS dengan Data Hipotetis
Misalkan kita memiliki data hipotetis berikut untuk menganalisis pengaruh jumlah iklan (X 1) dan harga produk (X 2) terhadap penjualan (Y):
| Penjualan (Y) | Jumlah Iklan (X1) | Harga Produk (X2) |
|---|---|---|
| 10 | 2 | 100 |
| 15 | 3 | 90 |
| 20 | 4 | 80 |
| 25 | 5 | 70 |
Dengan menggunakan perangkat lunak statistik, kita akan mendapatkan estimasi koefisien regresi. Misalkan hasil estimasi adalah: Y = 5 + 2X 1
-0.1X 2. Ini berarti setiap penambahan satu unit iklan akan meningkatkan penjualan sebesar 2 unit, sementara setiap kenaikan harga sebesar 1 unit akan menurunkan penjualan sebesar 0.1 unit. Konstanta 5 merepresentasikan penjualan jika jumlah iklan dan harga produk adalah nol.
Interpretasi Hasil Estimasi Parameter
Koefisien regresi (β 1 dan β 2) menunjukkan pengaruh masing-masing variabel independen terhadap variabel dependen. Tanda positif menunjukkan hubungan positif (semakin besar variabel independen, semakin besar variabel dependen), sedangkan tanda negatif menunjukkan hubungan negatif. Besarnya koefisien menunjukkan kekuatan pengaruh tersebut. Konstanta (β 0) menunjukkan nilai variabel dependen ketika semua variabel independen bernilai nol. Interpretasi ini harus selalu mempertimbangkan konteks data dan model yang digunakan.
Pengujian Hipotesis
Setelah model regresi berganda dibangun, langkah selanjutnya adalah melakukan pengujian hipotesis untuk menilai signifikansi model dan koefisien regresi. Pengujian ini bertujuan untuk menentukan apakah model yang dibangun mampu menjelaskan variasi variabel dependen secara signifikan, dan apakah masing-masing variabel independen memberikan kontribusi yang signifikan terhadap variasi tersebut. Proses ini melibatkan uji statistik tertentu yang akan dijelaskan lebih lanjut di bawah ini.
Signifikansi Model Regresi Berganda Secara Keseluruhan
Pengujian signifikansi model secara keseluruhan dilakukan untuk menguji apakah setidaknya satu dari variabel independen memiliki pengaruh signifikan terhadap variabel dependen. Uji statistik yang digunakan adalah uji F. Hipotesis nol (H0) menyatakan bahwa semua koefisien regresi sama dengan nol (tidak ada pengaruh variabel independen terhadap variabel dependen), sedangkan hipotesis alternatif (H1) menyatakan bahwa setidaknya satu koefisien regresi tidak sama dengan nol (ada pengaruh setidaknya satu variabel independen).
Nilai p yang dihasilkan dari uji F dibandingkan dengan tingkat signifikansi (α, biasanya 0.05). Jika nilai p kurang dari α, maka H0 ditolak, yang berarti model regresi secara keseluruhan signifikan.
Signifikansi Masing-Masing Koefisien Regresi
Setelah menguji signifikansi model secara keseluruhan, langkah selanjutnya adalah menguji signifikansi masing-masing koefisien regresi. Uji ini bertujuan untuk menentukan apakah setiap variabel independen secara individual berkontribusi signifikan terhadap model. Uji statistik yang digunakan adalah uji t. Hipotesis nol (H0) untuk setiap koefisien adalah bahwa koefisien tersebut sama dengan nol (tidak ada pengaruh variabel independen tersebut terhadap variabel dependen), sedangkan hipotesis alternatif (H1) menyatakan bahwa koefisien tersebut tidak sama dengan nol (ada pengaruh variabel independen tersebut).
Nilai p dari uji t untuk setiap koefisien dibandingkan dengan tingkat signifikansi (α). Jika nilai p kurang dari α, maka H0 ditolak, menunjukkan bahwa variabel independen tersebut signifikan secara statistik.
Uji Statistik yang Digunakan
Seperti yang telah dijelaskan sebelumnya, uji F digunakan untuk menguji signifikansi model secara keseluruhan, sedangkan uji t digunakan untuk menguji signifikansi masing-masing koefisien regresi. Kedua uji ini menghasilkan nilai statistik uji dan nilai p yang digunakan untuk pengambilan keputusan.
Tabel Ringkasan Hasil Pengujian Hipotesis
Berikut contoh tabel yang merangkum hasil pengujian hipotesis. Perlu diingat bahwa nilai-nilai ini hanyalah ilustrasi dan akan berbeda untuk setiap model regresi.
| Variabel | Koefisien Regresi | Nilai t | Nilai p | Kesimpulan |
|---|---|---|---|---|
| Konstanta | 10.5 | – | – | – |
| X1 | 2.3 | 3.5 | 0.002 | Signifikan |
| X2 | -1.2 | -1.8 | 0.08 | Tidak Signifikan |
| X3 | 0.8 | 2.1 | 0.04 | Signifikan |
| Uji F (Model Keseluruhan) | – | 6.2 | 0.005 | Signifikan |
Pada contoh di atas, variabel X1 dan X3 signifikan secara statistik karena nilai p kurang dari 0.05, sedangkan X2 tidak signifikan.
Interpretasi Nilai R-squared dan Adjusted R-squared
Nilai R-squared menunjukkan proporsi variansi variabel dependen yang dijelaskan oleh model regresi. Nilai yang lebih tinggi menandakan model yang lebih baik dalam menjelaskan data. Namun, R-squared dapat meningkat secara artifisial dengan penambahan variabel independen, meskipun variabel tersebut tidak signifikan. Oleh karena itu, Adjusted R-squared seringkali lebih disukai karena mengoreksi pengaruh jumlah variabel independen terhadap R-squared. Nilai Adjusted R-squared yang lebih tinggi menunjukkan model yang lebih baik setelah memperhitungkan jumlah variabel.
Interpretasi Hasil Analisis: Analisis Regresi Berganda
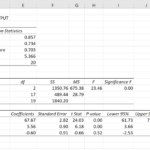
Setelah menjalankan analisis regresi berganda, langkah selanjutnya adalah menginterpretasi hasil yang diperoleh. Interpretasi ini akan memberikan pemahaman mengenai hubungan antara variabel dependen dan variabel independen yang diteliti, serta kekuatan dan signifikansi hubungan tersebut. Interpretasi yang tepat membutuhkan pemahaman yang baik terhadap output statistik yang dihasilkan oleh perangkat lunak analisis.
Contoh Output dan Penjelasannya
Misalnya, kita peroleh output regresi berganda sebagai berikut (data fiktif untuk ilustrasi):
Variabel Dependen: Penjualan (dalam jutaan rupiah)
| Variabel Independen | Koefisien | t-statistik | p-value |
|---|---|---|---|
| Biaya Periklanan (dalam jutaan rupiah) | 0.8 | 5.2 | 0.001 |
| Harga Produk (dalam ribuan rupiah) | -0.2 | -2.1 | 0.05 |
| Konstanta | 10 |
Dari tabel di atas, koefisien untuk Biaya Periklanan adalah 0.8. Ini berarti setiap peningkatan 1 juta rupiah dalam biaya periklanan diprediksi akan meningkatkan penjualan sebesar 0.8 juta rupiah, dengan asumsi variabel lain konstan. Koefisien untuk Harga Produk adalah -0.2, menunjukkan bahwa setiap kenaikan harga produk sebesar 1000 rupiah diprediksi akan menurunkan penjualan sebesar 0.2 juta rupiah, dengan asumsi variabel lain konstan.
Nilai t-statistik dan p-value digunakan untuk menguji signifikansi statistik koefisien.
Identifikasi Variabel Independen yang Signifikan Secara Statistik
Signifikansi statistik suatu variabel independen diuji melalui p-value. Secara umum, jika p-value kurang dari 0.05 (tingkat signifikansi umum), maka variabel independen tersebut dianggap signifikan secara statistik. Dalam contoh di atas, Biaya Periklanan (p-value = 0.001 < 0.05) signifikan secara statistik, sementara Harga Produk (p-value = 0.05) berada di batas signifikansi. Ini menunjukkan bahwa pengaruh Biaya Periklanan terhadap Penjualan lebih kuat dan konsisten dibandingkan dengan pengaruh Harga Produk.
Pengukuran Kekuatan Hubungan Antara Variabel Dependen dan Independen
Kekuatan hubungan antara variabel dependen dan independen dapat diukur menggunakan R-squared (R²). R² menunjukkan proporsi variansi variabel dependen yang dijelaskan oleh variabel independen dalam model. Nilai R² berkisar antara 0 dan 1, dengan nilai yang mendekati 1 menunjukkan hubungan yang lebih kuat. Misalnya, jika R² = 0.7, maka 70% variansi dalam Penjualan dapat dijelaskan oleh Biaya Periklanan dan Harga Produk dalam model regresi ini.
Selain R², Adjusted R² juga sering digunakan, terutama saat terdapat banyak variabel independen, karena Adjusted R² memperhitungkan jumlah variabel dalam model.
Contoh Kasus dan Langkah-Langkah Analisis Regresi Berganda
Sebuah perusahaan ritel ingin mengetahui faktor-faktor yang mempengaruhi penjualan produknya. Data yang dikumpulkan meliputi penjualan (variabel dependen), biaya iklan, harga produk, dan jumlah promosi yang dilakukan (variabel independen). Langkah-langkah analisis regresi berganda:
- Pengumpulan Data: Mengumpulkan data penjualan, biaya iklan, harga produk, dan jumlah promosi selama periode tertentu.
- Pemilihan Model: Memilih model regresi berganda yang sesuai dengan data dan tujuan analisis.
- Estimasi Parameter: Menggunakan perangkat lunak statistik untuk mengestimasi koefisien regresi.
- Pengujian Asumsi: Memeriksa apakah asumsi-asumsi regresi berganda terpenuhi (misalnya, linearitas, normalitas residual, homoskedastisitas).
- Interpretasi Hasil: Menganalisis koefisien regresi, p-value, dan R² untuk memahami hubungan antara variabel dependen dan independen.
Laporan Singkat Hasil Analisis Regresi Berganda
Analisis regresi berganda menunjukkan bahwa Biaya Periklanan memiliki pengaruh signifikan dan positif terhadap Penjualan. Sebaliknya, pengaruh Harga Produk terhadap Penjualan signifikan tetapi negatif. Model regresi menjelaskan 70% variansi dalam Penjualan (R² = 0.7). Namun, model ini memiliki keterbatasan karena hanya mempertimbangkan beberapa variabel, dan mungkin terdapat variabel lain yang mempengaruhi penjualan yang belum dimasukkan dalam model. Hasil analisis ini dapat digunakan untuk mengoptimalkan strategi pemasaran dengan mengalokasikan anggaran iklan secara efektif dan menentukan harga produk yang optimal.
Ringkasan Penutup
Analisis regresi berganda terbukti menjadi alat yang sangat berharga dalam berbagai bidang, dari ekonomi dan bisnis hingga ilmu sosial dan kesehatan. Kemampuannya untuk mempertimbangkan beberapa variabel independen sekaligus memberikan wawasan yang lebih kaya dan prediksi yang lebih akurat. Namun, penting untuk selalu mengingat asumsi-asumsi dasar dan keterbatasan model untuk menghindari interpretasi yang keliru. Dengan pemahaman yang baik tentang metodologi dan interpretasinya, analisis regresi berganda dapat menjadi kunci untuk mengungkap pola-pola tersembunyi dalam data dan mendukung pengambilan keputusan yang lebih baik.