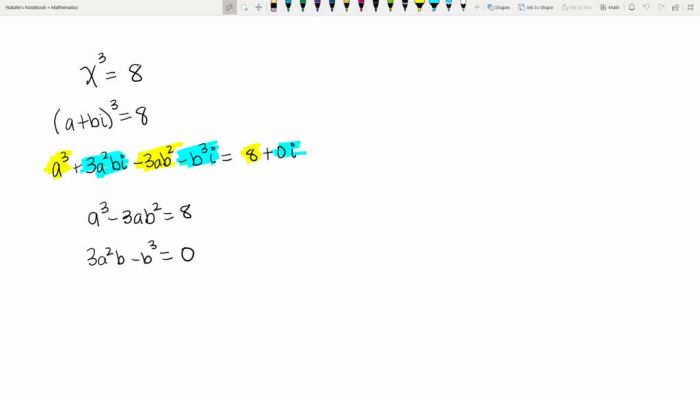
- Memahami “Analisis Real”
- Konsep-Konsep Utama dalam “Analisis Real”
- Penerapan “Analisis Real” dalam Berbagai Bidang
-
Teknik dan Metode dalam Analisis Real
- Contoh Penggunaan Metode Numerik dalam Analisis Real
- Langkah-langkah Penyelesaian Persamaan Diferensial Menggunakan Teknik Analisis Real
- Perbedaan Metode Analitik dan Numerik dalam Analisis Real
- Kutipan Ahli Matematika Mengenai Pentingnya Analisis Real
- Software dan Tools untuk Perhitungan dalam Analisis Real
- Kesimpulan
Analisis real merupakan cabang matematika yang mendasari banyak bidang ilmu lainnya. Ia menjelajahi dunia bilangan real, limit, kontinuitas, turunan, dan integral, membentuk fondasi bagi pemahaman yang lebih dalam tentang perubahan dan proses kontinu. Dari prediksi cuaca hingga pemodelan ekonomi, analisis real menyediakan alat-alat matematis yang ampuh untuk menganalisis dan memecahkan permasalahan kompleks di berbagai disiplin ilmu.
Kajian ini akan membahas definisi analisis real, membandingkannya dengan analisis kompleks dan numerik, serta menelusuri penerapannya dalam fisika, ekonomi, dan teknik. Konsep-konsep kunci seperti limit, kontinuitas, turunan, dan integral akan diuraikan secara detail, disertai contoh-contoh penerapan dan penyelesaian soal. Tantangan dan peluang analisis real di era big data juga akan dibahas.
Memahami “Analisis Real”
Analisis real merupakan cabang matematika yang mempelajari bilangan real, limit, turunan, integral, dan deret tak hingga. Ia membentuk fondasi bagi banyak bidang ilmu, termasuk kalkulus, persamaan diferensial, dan probabilitas. Pemahaman mendalam tentang analisis real sangat krusial dalam membangun model matematika yang akurat dan menyelesaikan berbagai permasalahan di berbagai disiplin ilmu.
Definisi Analisis Real
Analisis real secara formal didefinisikan sebagai studi tentang himpunan bilangan real dan fungsi-fungsi yang didefinisikan pada himpunan tersebut. Ia berfokus pada sifat-sifat kontinuitas, diferensial, dan integral fungsi-fungsi real, serta konsep-konsep limit dan konvergensi. Analisis real menyediakan kerangka kerja yang ketat untuk menyelidiki perilaku fungsi dan menyelesaikan permasalahan yang melibatkan perubahan kontinu.
Penerapan Analisis Real dalam Ilmu Komputer
Analisis real memiliki peran penting dalam berbagai aspek ilmu komputer. Salah satu penerapannya yang signifikan adalah dalam pengembangan algoritma dan pemodelan sistem. Misalnya, dalam grafik komputer, analisis real digunakan untuk menghitung pencahayaan dan bayangan yang realistis. Analisis real juga mendasari algoritma optimasi yang digunakan dalam machine learning dan kecerdasan buatan, membantu dalam menemukan solusi optimal untuk masalah kompleks.
Lebih lanjut, analisis real berperan dalam pemodelan dan simulasi sistem fisik, seperti dalam dinamika fluida komputasional atau simulasi robot.
Perbedaan Analisis Real dan Analisis Kompleks
Analisis real dan analisis kompleks merupakan dua cabang analisis matematika yang saling berkaitan namun berbeda fokus. Analisis real berfokus pada bilangan real dan fungsi-fungsi bernilai real, sementara analisis kompleks mempelajari bilangan kompleks dan fungsi-fungsi bernilai kompleks. Analisis kompleks memperluas konsep-konsep dari analisis real ke bidang kompleks, memperkenalkan konsep-konsep baru seperti fungsi analitik dan integral kontur, yang tidak ditemukan dalam analisis real.
Meskipun berbeda, banyak konsep dan teknik dalam analisis real menjadi dasar bagi analisis kompleks.
Perbandingan Analisis Real dan Analisis Numerik
Analisis real dan analisis numerik memiliki pendekatan berbeda dalam menyelesaikan permasalahan matematika. Analisis real menekankan pada solusi eksak dan sifat-sifat matematis, sementara analisis numerik fokus pada pendekatan numerik untuk memperoleh solusi hampiran. Berikut tabel perbandingannya:
| Nama Metode | Keunggulan | Kelemahan | Contoh Penerapan |
|---|---|---|---|
| Integrasi Definit (Analisis Real) | Memberikan solusi eksak (jika ada) | Tidak selalu mudah diterapkan untuk semua fungsi, terkadang rumit untuk dihitung secara analitis. | Menghitung luas daerah di bawah kurva. |
| Metode Trapesium (Analisis Numerik) | Mudah diterapkan, cocok untuk fungsi yang rumit. | Memberikan solusi hampiran, akurasi bergantung pada jumlah partisi. | Menghitung luas daerah di bawah kurva secara hampiran. |
| Mencari Titik Ekstrim (Analisis Real) | Menemukan titik ekstrim yang tepat. | Membutuhkan turunan dan analisis fungsi yang kompleks. | Optimasi fungsi dalam model matematika. |
| Metode Newton-Raphson (Analisis Numerik) | Efisien untuk mencari akar persamaan non-linear. | Tidak selalu konvergen, bergantung pada titik awal. | Mencari akar persamaan non-linear dalam simulasi. |
Langkah-langkah Dasar Analisis Real pada Suatu Permasalahan
Menerapkan analisis real pada suatu permasalahan umumnya melibatkan beberapa langkah. Langkah-langkah ini dapat bervariasi tergantung kompleksitas masalah, namun secara umum meliputi:
- Rumusan Masalah: Mendefinisikan permasalahan secara matematis, mengidentifikasi variabel dan parameter yang terlibat.
- Pembentukan Model Matematika: Membangun model matematika yang merepresentasikan permasalahan, mungkin melibatkan persamaan diferensial, integral, atau sistem persamaan.
- Analisis Matematika: Menerapkan teknik-teknik analisis real, seperti kalkulus, untuk menganalisis model matematika dan mencari solusi.
- Interpretasi Hasil: Menerjemahkan solusi matematis ke dalam konteks permasalahan asli, dan mengevaluasi validitas dan implikasi solusi.
- Validasi dan Verifikasi: Membandingkan hasil analisis dengan data empiris atau simulasi untuk memvalidasi model dan solusi yang diperoleh.
Konsep-Konsep Utama dalam “Analisis Real”

Analisis real merupakan cabang matematika yang mendasari banyak bidang ilmu lainnya, seperti kalkulus, persamaan diferensial, dan analisis numerik. Pemahaman yang kuat terhadap konsep-konsep utamanya sangat krusial untuk menguasai bidang-bidang tersebut. Berikut uraian beberapa konsep kunci dalam analisis real.
Limit dan Kontinuitas
Limit dan kontinuitas merupakan dua konsep fundamental dalam analisis real. Limit suatu fungsi menggambarkan nilai yang didekati oleh fungsi tersebut ketika variabel bebas mendekati suatu nilai tertentu. Sementara itu, kontinuitas menggambarkan kelancaran fungsi tanpa adanya lompatan atau diskontinuitas. Secara formal, sebuah fungsi dikatakan kontinu di suatu titik jika limit fungsi di titik tersebut sama dengan nilai fungsi di titik tersebut.
Konsep limit menjadi dasar dalam mendefinisikan turunan dan integral.
Turunan dan Integral
Turunan suatu fungsi merepresentasikan laju perubahan instan fungsi tersebut terhadap perubahan variabel bebasnya. Secara geometris, turunan mewakili kemiringan garis singgung kurva fungsi pada suatu titik. Integral, di sisi lain, merepresentasikan luas daerah di bawah kurva fungsi. Teorema Fundamental Kalkulus menghubungkan turunan dan integral, menyatakan bahwa integral tak tentu suatu fungsi merupakan antiturunannya, dan integral tentu dapat dihitung menggunakan antiturunan.
Hubungan ini sangat penting dalam menyelesaikan berbagai permasalahan matematika dan fisika.
Deret dan Konvergensinya
Deret dalam analisis real adalah penjumlahan tak hingga dari suku-suku. Konvergensi deret merujuk pada apakah penjumlahan tak hingga tersebut menghasilkan nilai yang terbatas atau tidak. Ada berbagai macam uji konvergensi, seperti uji banding, uji rasio, dan uji integral, yang digunakan untuk menentukan konvergensi suatu deret. Konsep deret sangat penting dalam berbagai aplikasi, seperti penyelesaian persamaan diferensial dan representasi fungsi dalam bentuk deret Taylor atau Fourier.
Contoh Soal dan Penyelesaian: Limit dan Kontinuitas
Berikut contoh soal yang melibatkan konsep limit dan kontinuitas:
Tentukan limit dari fungsi f(x) = (x²
-4) / (x – 2) ketika x mendekati 2.
Penyelesaian:
Jika kita langsung substitusikan x = 2 ke dalam fungsi, kita akan mendapatkan bentuk tak tentu 0/
0. Oleh karena itu, kita perlu menyederhanakan fungsi tersebut terlebih dahulu:
f(x) = (x²
4) / (x – 2) = (x – 2)(x + 2) / (x – 2) = x + 2
Sekarang, kita dapat menghitung limitnya:
lim (x→2) f(x) = lim (x→2) (x + 2) = 2 + 2 = 4
Jadi, limit dari fungsi f(x) ketika x mendekati 2 adalah 4.
Penerapan Teorema Nilai Tengah
Teorema Nilai Tengah (Mean Value Theorem) menyatakan bahwa untuk suatu fungsi kontinu pada interval tertutup [a, b] dan terdiferensialkan pada interval buka (a, b), terdapat setidaknya satu titik c di dalam (a, b) sedemikian sehingga f'(c) = (f(b)
- f(a)) / (b – a). Artinya, terdapat titik di mana kemiringan garis singgung kurva sama dengan kemiringan garis penghubung antara titik (a, f(a)) dan (b, f(b)). Sebagai contoh, perhatikan fungsi f(x) = x² pada interval [1, 3]. Turunannya adalah f'(x) = 2x. Menurut Teorema Nilai Tengah, terdapat titik c di (1, 3) sedemikian sehingga 2c = (3²
- 1²) / (3 – 1) = 8 / 2 = 4. Oleh karena itu, c = 2, yang berada di dalam interval (1, 3).
Penerapan “Analisis Real” dalam Berbagai Bidang

Analisis real, dengan landasannya pada konsep limit, kekontinuan, dan turunan, memiliki penerapan luas dan mendalam di berbagai disiplin ilmu. Kemampuannya dalam memodelkan fenomena kontinu dan perubahan secara presisi menjadikannya alat yang tak tergantikan dalam berbagai bidang, dari fisika hingga ekonomi dan teknik. Berikut beberapa contoh penerapannya.
Analisis Real dalam Mekanika Klasik
Analisis real membentuk dasar pemahaman mekanika klasik. Konsep-konsep seperti kecepatan dan percepatan, yang merupakan turunan dari posisi terhadap waktu, didefinisikan dan dihitung menggunakan kalkulus, cabang matematika yang berakar pada analisis real. Misalnya, hukum gerak Newton, yang mendeskripsikan bagaimana gaya memengaruhi gerakan suatu objek, bergantung pada konsep turunan untuk menghitung percepatan. Perhitungan lintasan proyektil, pergerakan pendulum, dan dinamika sistem mekanik lainnya secara luas bergantung pada penerapan konsep-konsep limit dan turunan dari analisis real.
Peran Analisis Real dalam Pemodelan Ekonomi
Dalam ekonomi, analisis real digunakan untuk memodelkan berbagai fenomena ekonomi, khususnya yang melibatkan perubahan kontinu. Misalnya, kurva penawaran dan permintaan, yang menggambarkan hubungan antara harga dan kuantitas barang yang ditawarkan dan diminta, seringkali dimodelkan menggunakan fungsi kontinu. Analisis real memungkinkan ekonom untuk menganalisis titik keseimbangan pasar, elastisitas permintaan, dan dampak perubahan kebijakan ekonomi terhadap variabel ekonomi lainnya. Lebih lanjut, teori pertumbuhan ekonomi dan optimasi sumber daya juga memanfaatkan konsep-konsep analisis real untuk membuat prediksi dan menganalisis skenario ekonomi.
Penggunaan Analisis Real dalam Prediksi Pola Cuaca
Prediksi pola cuaca merupakan contoh yang kompleks dari penerapan analisis real. Model cuaca numerik, yang digunakan oleh meteorologis untuk memprediksi cuaca, didasarkan pada persamaan diferensial parsial yang menggambarkan dinamika atmosfer. Persamaan-persamaan ini didasarkan pada hukum-hukum fisika yang mendeskripsikan pergerakan udara, transfer panas, dan kelembapan. Analisis real menyediakan kerangka kerja matematika untuk menyelesaikan persamaan-persamaan ini, dan untuk menafsirkan hasilnya.
Sebagai contoh, permodelan pergerakan massa udara panas dan dingin yang saling berinteraksi memerlukan penggunaan konsep-konsep limit dan turunan untuk menghitung perubahan tekanan, suhu, dan kecepatan angin secara akurat. Model-model tersebut membagi atmosfer menjadi grid tiga dimensi, dan menggunakan persamaan diferensial parsial untuk menghitung perubahan kondisi cuaca di setiap titik grid pada selang waktu tertentu. Akurasi prediksi bergantung pada resolusi grid, akurasi data input, dan kompleksitas model yang digunakan.
Semakin detail grid dan semakin kompleks modelnya, semakin akurat (tetapi juga semakin berat komputasinya) prediksi cuaca yang dihasilkan. Sebagai contoh konkret, prediksi badai siklon tropis memerlukan permodelan yang sangat detail mengenai interaksi antara suhu permukaan laut, kelembapan udara, dan kecepatan angin, yang semuanya memerlukan analisis real yang canggih.
Penerapan Analisis Real dalam Teknik Sipil
Dalam teknik sipil, analisis real digunakan untuk menganalisis dan merancang struktur seperti jembatan, gedung, dan bendungan. Misalnya, perhitungan tegangan dan regangan pada struktur, yang penting untuk memastikan keamanan dan stabilitasnya, melibatkan penerapan kalkulus integral dan diferensial. Analisis elemen hingga, sebuah metode numerik yang digunakan secara luas dalam teknik sipil, bergantung pada konsep-konsep analisis real untuk mendekati solusi persamaan diferensial yang menggambarkan perilaku struktur di bawah beban.
Contoh penerapannya adalah perhitungan defleksi balok di bawah beban, di mana analisis real memungkinkan insinyur untuk menentukan apakah struktur mampu menahan beban yang diberikan tanpa mengalami kerusakan struktural.
Tantangan dan Peluang Analisis Real di Era Big Data
Era big data menghadirkan tantangan dan peluang baru bagi penerapan analisis real. Jumlah data yang sangat besar yang dihasilkan dari berbagai sumber memerlukan algoritma dan metode komputasi yang efisien untuk menganalisis data tersebut. Meskipun demikian, analisis real menyediakan kerangka kerja matematika yang kuat untuk mengembangkan algoritma tersebut. Tantangannya terletak pada pengembangan metode yang mampu menangani data yang tidak lengkap, bising, dan berdimensi tinggi.
Peluangnya terletak pada pengembangan model-model yang lebih akurat dan komprehensif, yang mampu menangkap kompleksitas fenomena nyata. Contohnya, dalam prediksi cuaca, penggunaan big data dari berbagai sensor, satelit, dan stasiun cuaca dapat meningkatkan akurasi prediksi cuaca. Namun, mengolah data dalam skala besar ini memerlukan metode komputasi yang efisien dan robust yang didasarkan pada prinsip-prinsip analisis real.
Teknik dan Metode dalam Analisis Real

Analisis real, sebagai cabang matematika yang mempelajari bilangan real dan fungsi-fungsi di atasnya, menawarkan berbagai teknik dan metode untuk menyelesaikan permasalahan matematika yang kompleks. Pemahaman yang mendalam terhadap teknik-teknik ini sangat krusial dalam berbagai bidang, mulai dari fisika dan teknik hingga ekonomi dan ilmu komputer. Berikut ini akan dibahas beberapa teknik dan metode penting dalam analisis real, beserta contoh penerapannya.
Contoh Penggunaan Metode Numerik dalam Analisis Real
Metode numerik memberikan pendekatan solusi hampiran untuk masalah yang sulit atau bahkan tidak mungkin diselesaikan secara analitik. Dalam analisis real, metode ini sering digunakan untuk menyelesaikan persamaan diferensial, integral, dan optimasi. Sebagai contoh, metode Euler merupakan metode numerik sederhana untuk menyelesaikan persamaan diferensial biasa. Metode ini memberikan pendekatan solusi dengan langkah-langkah iteratif, menghitung nilai fungsi pada titik berikutnya berdasarkan gradien di titik sebelumnya.
Meskipun sederhana, metode Euler dapat memberikan hasil yang cukup akurat untuk beberapa kasus, terutama jika langkah iterasi yang digunakan cukup kecil. Metode numerik yang lebih canggih, seperti metode Runge-Kutta, menawarkan akurasi yang lebih tinggi dengan kompleksitas komputasi yang lebih besar.
Langkah-langkah Penyelesaian Persamaan Diferensial Menggunakan Teknik Analisis Real
Penyelesaian persamaan diferensial dalam analisis real seringkali melibatkan penggunaan teknik seperti pemisahan variabel, faktor integral, atau transformasi Laplace. Langkah-langkah umum yang terlibat tergantung pada jenis persamaan diferensial yang dihadapi. Sebagai ilustrasi, perhatikan persamaan diferensial orde pertama sederhana dy/dx = f(x). Langkah penyelesaiannya dapat berupa integrasi langsung kedua ruas persamaan terhadap x. Untuk persamaan diferensial orde lebih tinggi atau persamaan diferensial parsial, teknik yang lebih kompleks diperlukan, melibatkan konsep-konsep seperti ruang vektor, transformasi integral, dan deret fungsi.
- Identifikasi jenis persamaan diferensial.
- Pilih metode yang sesuai (misalnya, pemisahan variabel, faktor integral, transformasi Laplace).
- Terapkan metode tersebut secara sistematis.
- Verifikasi solusi yang diperoleh.
Perbedaan Metode Analitik dan Numerik dalam Analisis Real
Metode analitik dan numerik menawarkan pendekatan yang berbeda dalam menyelesaikan masalah dalam analisis real. Metode analitik bertujuan untuk menemukan solusi eksak atau tertutup, sedangkan metode numerik memberikan solusi hampiran. Metode analitik seringkali melibatkan manipulasi aljabar dan kalkulus untuk mendapatkan solusi yang tepat, sementara metode numerik menggunakan algoritma dan komputasi untuk mendapatkan pendekatan solusi. Pilihan antara metode analitik dan numerik bergantung pada kompleksitas masalah, kebutuhan akurasi, dan ketersediaan sumber daya komputasi.
| Metode | Karakteristik | Contoh |
|---|---|---|
| Analitik | Mencari solusi eksak, seringkali melibatkan manipulasi aljabar dan kalkulus. | Integrasi langsung, pemisahan variabel. |
| Numerik | Mencari solusi hampiran, menggunakan algoritma dan komputasi. | Metode Euler, metode Runge-Kutta. |
Kutipan Ahli Matematika Mengenai Pentingnya Analisis Real
“Analisis real adalah fondasi bagi sebagian besar matematika modern. Pemahaman yang mendalam tentang konsep-konsep dasar analisis real sangat penting bagi siapa pun yang ingin mempelajari matematika tingkat lanjut.”(Nama Ahli Matematika dan Referensi, jika tersedia. Jika tidak, ganti dengan pernyataan umum yang sesuai)
Software dan Tools untuk Perhitungan dalam Analisis Real
Sejumlah perangkat lunak dan tools dapat membantu dalam melakukan perhitungan dan visualisasi dalam analisis real. Beberapa contohnya termasuk:
- MATLAB: Merupakan software komputasi numerik yang kuat dan serbaguna, sering digunakan untuk menyelesaikan persamaan diferensial dan melakukan berbagai analisis numerik lainnya.
- Maple dan Mathematica: Sistem aljabar komputer (CAS) yang mampu melakukan perhitungan simbolik dan numerik yang kompleks, termasuk manipulasi aljabar dan kalkulus.
- Python dengan library seperti NumPy dan SciPy: Bahasa pemrograman yang fleksibel dan kuat, dengan library yang menyediakan berbagai fungsi untuk komputasi numerik dan visualisasi data.
Kesimpulan
Analisis real, dengan kekayaan konsep dan penerapannya yang luas, terbukti menjadi pilar penting dalam perkembangan ilmu pengetahuan dan teknologi. Pemahaman mendalam tentang limit, kontinuitas, dan kalkulus merupakan kunci untuk memecahkan masalah kompleks di berbagai bidang. Meskipun tantangan dalam penerapannya terus berkembang seiring dengan era big data, potensi analisis real untuk memberikan wawasan dan solusi yang inovatif tetap tak terbantahkan.