Analisis biplot merupakan teknik visualisasi data multivariat yang ampuh untuk memahami hubungan kompleks antar variabel dan observasi. Dengan memadukan informasi dari berbagai variabel dalam satu diagram, biplot memberikan gambaran yang intuitif dan mudah dipahami, sehingga membantu peneliti dalam menarik kesimpulan yang bermakna. Teknik ini telah diaplikasikan secara luas di berbagai bidang, mulai dari analisis genetika hingga penelitian pasar, membuktikan fleksibilitas dan kegunaannya dalam mengolah data yang kompleks.
Biplot memungkinkan visualisasi simultan dari variabel dan observasi dalam ruang dimensi rendah. Vektor variabel merepresentasikan arah dan besar pengaruh variabel, sementara titik observasi menunjukkan posisi relatif observasi berdasarkan variabel-variabel tersebut. Dengan memahami posisi relatif vektor dan titik, kita dapat menganalisis korelasi antar variabel, serta mengklasifikasikan dan membandingkan observasi. Pemahaman yang mendalam tentang biplot akan memberikan kemampuan untuk mengolah dan menginterpretasi data multivariat dengan lebih efektif.
Pengenalan Biplot
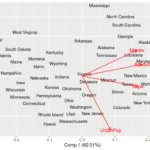
Biplot merupakan teknik visualisasi data multivariat yang efektif untuk menampilkan hubungan simultan antara variabel dan observasi dalam suatu dataset. Ia memadukan informasi dari berbagai variabel ke dalam suatu grafik dua dimensi, sehingga memudahkan interpretasi pola dan hubungan yang kompleks. Kemampuannya untuk menampilkan data multivariat dalam ruang dua dimensi membuatnya menjadi alat yang berharga dalam berbagai bidang ilmu.
Tujuan utama penggunaan biplot adalah untuk memvisualisasikan struktur data multivariat secara ringkas dan mudah dipahami. Dengan menampilkan baik variabel maupun observasi dalam satu plot, biplot memungkinkan identifikasi pola, kelompok, dan hubungan antar variabel serta hubungan antara variabel dan observasi. Hal ini sangat membantu dalam pengambilan kesimpulan dan pemahaman yang lebih mendalam terhadap data.
Penerapan Biplot dalam Berbagai Bidang
Biplot telah diaplikasikan secara luas di berbagai disiplin ilmu. Berikut beberapa contohnya:
- Analisis Genetika: Biplot dapat digunakan untuk memvisualisasikan hubungan antara gen dan fenotipe, membantu dalam identifikasi gen yang terkait dengan sifat tertentu. Misalnya, dalam studi tentang ekspresi gen, biplot dapat menunjukkan gen mana yang memiliki ekspresi tinggi atau rendah pada kelompok individu tertentu.
- Ekonomi: Dalam ekonomi, biplot dapat digunakan untuk menganalisis hubungan antara berbagai variabel ekonomi, seperti inflasi, suku bunga, dan pertumbuhan ekonomi. Hal ini dapat membantu dalam memahami dinamika ekonomi dan membuat prediksi.
- Ilmu Lingkungan: Biplot dapat digunakan untuk memvisualisasikan hubungan antara berbagai polutan dan kualitas lingkungan. Misalnya, dapat menunjukkan hubungan antara konsentrasi polutan dan indeks kualitas air.
Perbandingan Biplot dengan Teknik Visualisasi Data Multivariat Lainnya
Berikut tabel perbandingan biplot dengan teknik visualisasi data multivariat lainnya, seperti PCA plot:
| Teknik | Keunggulan | Kelemahan | Aplikasi |
|---|---|---|---|
| Biplot | Menampilkan hubungan antara variabel dan observasi secara simultan dalam satu plot; mudah diinterpretasi; relatif sederhana | Informasi dapat hilang dalam reduksi dimensi; interpretasi dapat menjadi kompleks jika terdapat banyak variabel; akurasi bergantung pada kualitas data | Analisis genetika, ekonomi, ilmu lingkungan, ilmu sosial |
| PCA Plot | Menunjukkan variasi data dalam ruang dimensi rendah; efektif untuk reduksi dimensi; mudah untuk mengidentifikasi komponen utama | Tidak menampilkan hubungan antara variabel secara langsung; interpretasi komponen utama dapat sulit; perlu interpretasi tambahan untuk memahami hubungan antar variabel | Pengolahan citra, analisis data genetik, analisis data sensor |
Ilustrasi Biplot Sederhana
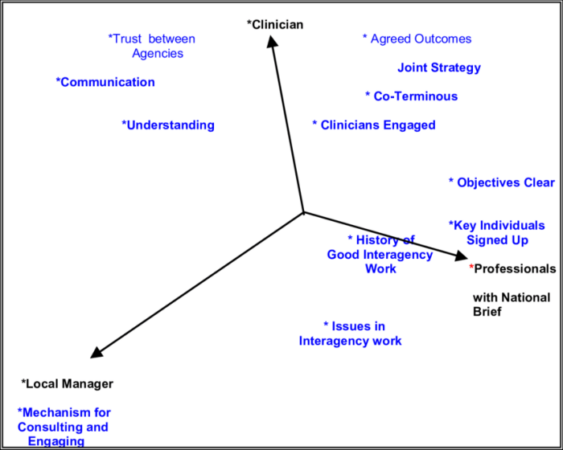
Bayangkan sebuah biplot sederhana dengan dua sumbu, sumbu X dan sumbu Y. Vektor variabel direpresentasikan sebagai panah yang keluar dari titik asal (0,0). Panjang vektor menunjukkan besarnya pengaruh variabel, sedangkan arah vektor menunjukkan korelasi antara variabel. Titik observasi diplot di dalam ruang yang dibentuk oleh vektor variabel. Jarak antara titik observasi menunjukkan kemiripan atau perbedaan antara observasi.
Semakin dekat titik observasi dengan suatu vektor variabel, semakin besar pengaruh variabel tersebut terhadap observasi tersebut. Sudut antara vektor variabel menunjukkan korelasi antara variabel; sudut kecil menunjukkan korelasi positif yang kuat, sudut besar menunjukkan korelasi negatif yang kuat, dan sudut 90 derajat menunjukkan tidak ada korelasi.
Sebagai contoh, misalkan terdapat dua variabel, X (pendapatan) dan Y (pengeluaran), dan tiga observasi (individu A, B, dan C). Vektor X dan Y akan menunjukkan arah dan besarnya pengaruh pendapatan dan pengeluaran. Titik A, B, dan C akan diplot berdasarkan nilai pendapatan dan pengeluaran mereka. Jika titik A dekat dengan vektor X, ini menunjukkan bahwa pendapatan memiliki pengaruh yang besar terhadap individu A.
Jika vektor X dan Y membentuk sudut kecil, ini menunjukkan korelasi positif antara pendapatan dan pengeluaran.
Interpretasi Biplot: Analisis Biplot
Biplot merupakan alat visualisasi data yang sangat berguna untuk memahami hubungan antara variabel dan observasi dalam suatu dataset. Ia menampilkan baik variabel maupun observasi dalam ruang dua dimensi, memungkinkan kita untuk mengidentifikasi pola dan hubungan yang mungkin tidak terlihat dalam tabel data mentah. Interpretasi biplot membutuhkan pemahaman tentang elemen-elemen kunci dan bagaimana posisi relatif mereka mencerminkan korelasi dan klasifikasi.
Elemen Kunci dalam Biplot
Sebuah biplot terdiri dari dua elemen utama: vektor variabel dan titik observasi. Vektor variabel direpresentasikan sebagai garis yang memanjang dari pusat biplot, dengan arah dan panjang yang merepresentasikan arah dan kekuatan variabel tersebut. Titik observasi, di sisi lain, merepresentasikan setiap data point dalam dataset. Posisi relatif dari vektor variabel dan titik observasi memberikan informasi berharga tentang hubungan antar variabel dan klasifikasi observasi.
Korelasi Antar Variabel
Sudut antara dua vektor variabel menunjukkan korelasi antar variabel tersebut. Semakin kecil sudut antara dua vektor, semakin tinggi korelasi positif antar variabel. Sebaliknya, sudut yang mendekati 180 derajat menunjukkan korelasi negatif yang kuat. Jika dua vektor hampir tegak lurus (sudut mendekati 90 derajat), maka korelasi antar variabel tersebut rendah atau mendekati nol.
Contoh Hubungan Antar Variabel
Misalkan kita memiliki biplot yang menampilkan variabel “tinggi badan” dan “berat badan”. Jika vektor “tinggi badan” dan “berat badan” membentuk sudut kecil, ini menunjukkan korelasi positif yang kuat: individu dengan tinggi badan yang lebih tinggi cenderung memiliki berat badan yang lebih tinggi pula. Sebaliknya, jika vektor “tinggi badan” dan “jumlah jam tidur” membentuk sudut mendekati 90 derajat, maka korelasi antara keduanya rendah atau tidak ada.
Klasifikasi Observasi Berdasarkan Variabel
Posisi titik observasi relatif terhadap vektor variabel memberikan informasi tentang nilai variabel tersebut untuk observasi tertentu. Sebuah titik observasi yang terletak dekat dengan ujung vektor variabel menunjukkan nilai tinggi untuk variabel tersebut, sementara titik observasi yang terletak jauh dari ujung vektor menunjukkan nilai rendah. Dengan menganalisis posisi relatif titik observasi terhadap berbagai vektor variabel, kita dapat mengklasifikasikan observasi berdasarkan kombinasi nilai variabel.
Contoh Kasus Interpretasi Biplot dengan Data Fiktif
Bayangkan sebuah biplot yang menggambarkan data penjualan produk di tiga toko berbeda (“Toko A”, “Toko B”, “Toko C”) berdasarkan dua variabel: “Harga” dan “Promosi”. Toko A direpresentasikan oleh titik yang dekat dengan vektor “Promosi” dan agak jauh dari vektor “Harga”, menunjukkan penjualan tinggi di Toko A disebabkan oleh promosi yang intensif, meskipun harganya relatif tinggi. Toko B terletak di tengah-tengah, mengindikasikan performa penjualan yang seimbang antara harga dan promosi.
Toko C terletak dekat vektor “Harga” dan jauh dari vektor “Promosi”, menunjukkan penjualan yang bergantung pada harga yang kompetitif.
Pembuatan Biplot
Biplot merupakan teknik visualisasi data yang sangat berguna untuk mengeksplorasi hubungan antara variabel dan observasi dalam dataset multivariat. Ia memadukan informasi dari matriks data dan matriks kovariansinya ke dalam sebuah diagram dua dimensi, sehingga memungkinkan kita untuk mengidentifikasi pola, hubungan, dan outlier dengan mudah. Pembuatan biplot dapat dilakukan menggunakan berbagai perangkat lunak statistik, dan pilihan metode dan parameter akan memengaruhi kualitas dan interpretasi visualisasi akhir.
Berikut ini akan dijelaskan langkah-langkah pembuatan biplot, jenis data yang sesuai, contoh kode, dan teknik optimasi tampilannya.
Langkah-langkah Pembuatan Biplot
Pembuatan biplot umumnya melibatkan beberapa langkah utama. Pertama, data perlu diproses dan dipreparasi, misalnya dengan standarisasi atau penskalaan. Kemudian, teknik reduksi dimensi seperti Analisis Komponen Utama (PCA) atau Analisis Korespondensi (CA) diterapkan untuk memproyeksikan data ke ruang dimensi rendah (biasanya dua dimensi). Terakhir, hasil proyeksi tersebut divisualisasikan sebagai biplot, di mana vektor mewakili variabel dan titik mewakili observasi.
Perangkat lunak statistik seperti R dan Python menyediakan fungsi-fungsi yang memudahkan proses ini.
- Pra-pemrosesan Data: Data perlu dibersihkan dan distandarisasi untuk memastikan setiap variabel berkontribusi secara seimbang pada analisis. Metode standarisasi seperti z-score sering digunakan.
- Reduksi Dimensi: PCA atau CA digunakan untuk mengurangi dimensi data ke dua dimensi utama yang menjelaskan varians terbesar dalam data. Hasilnya adalah skor komponen utama untuk setiap observasi dan loading untuk setiap variabel.
- Pembuatan Plot: Skor komponen utama diplot sebagai titik, sedangkan loading variabel diplot sebagai vektor. Posisi relatif titik dan vektor menunjukkan hubungan antara observasi dan variabel.
Jenis Data yang Cocok untuk Analisis Biplot
Biplot cocok untuk menganalisis data multivariat, khususnya data yang memiliki banyak variabel dan observasi. Jenis data yang umum dianalisis menggunakan biplot antara lain data yang bersifat numerik, baik kontinu maupun diskrit. Data kategorikal juga dapat dianalisis dengan menggunakan teknik seperti Analisis Korespondensi. Namun, penting untuk memastikan data tersebut telah diproses dan disiapkan dengan tepat sebelum analisis.
Contoh Kode (Pseudocode) untuk Pembuatan Biplot
Berikut adalah contoh pseudocode untuk membuat biplot menggunakan library PCA dalam Python:
# Impor library yang dibutuhkan
import pandas as pd
from sklearn.decomposition import PCA
import matplotlib.pyplot as plt
# Load data
data = pd.read_csv("data.csv")
# Standarisasi data
data_standardized = (data - data.mean()) / data.std()
# Lakukan PCA dengan 2 komponen
pca = PCA(n_components=2)
pca_result = pca.fit_transform(data_standardized)
# Buat biplot
plt.figure(figsize=(10, 8))
plt.scatter(pca_result[:, 0], pca_result[:, 1])
for i, col in enumerate(data.columns):
plt.arrow(0, 0, pca.components_[0, i], pca.components_[1, i], head_width=0.1, head_length=0.2)
plt.text(pca.components_[0, i], pca.components_[1, i], col)
plt.xlabel("Komponen Utama 1")
plt.ylabel("Komponen Utama 2")
plt.title("Biplot")
plt.show()
Metode Optimasi Tampilan Biplot, Analisis biplot
Untuk meningkatkan interpretasi biplot, beberapa metode optimasi dapat diterapkan. Misalnya, pemilihan skala yang tepat untuk sumbu x dan y sangat penting. Selain itu, penambahan label pada titik dan vektor, serta penggunaan warna dan bentuk yang berbeda dapat meningkatkan kejelasan visualisasi. Teknik-teknik ini membantu dalam mengidentifikasi pola dan hubungan yang tersembunyi dalam data dengan lebih mudah.
- Penskalaan yang Tepat: Skala sumbu harus dipilih sedemikian rupa sehingga baik vektor maupun titik terdistribusi dengan baik dan tidak terlalu berdekatan atau terlalu tersebar.
- Label dan Anotasi: Tambahkan label pada titik dan vektor untuk mengidentifikasi observasi dan variabel yang relevan.
- Warna dan Bentuk: Gunakan warna dan bentuk yang berbeda untuk membedakan kelompok observasi atau variabel.
Panduan Singkat Pemilihan Skala pada Biplot
Skala pada biplot harus dipilih dengan hati-hati agar visualisasi optimal. Jika vektor terlalu panjang atau pendek dibandingkan dengan jarak antar titik, interpretasi bisa menjadi sulit. Uji coba dengan berbagai skala dan perhatikan distribusi titik dan vektor untuk menemukan skala yang paling informatif. Pertimbangkan juga untuk menggunakan skala yang sama untuk sumbu x dan y untuk menghindari distorsi visual.
Keunggulan dan Keterbatasan Biplot
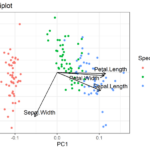
Biplot, sebagai teknik visualisasi data multivariat, menawarkan cara yang efisien untuk merepresentasikan hubungan antara variabel dan observasi secara simultan dalam ruang dimensi rendah. Namun, seperti metode visualisasi lainnya, biplot memiliki keunggulan dan keterbatasan yang perlu dipahami sebelum penerapannya. Pemahaman ini akan membantu peneliti dalam memilih metode yang paling tepat untuk menganalisis data mereka dan menghindari interpretasi yang salah.
Keunggulan Biplot
Biplot unggul dalam beberapa hal dibandingkan metode visualisasi data multivariat lainnya. Kemampuannya untuk menampilkan data multivariat dalam plot dua dimensi yang mudah dipahami menjadikannya alat yang sangat berharga. Berikut beberapa keunggulan utamanya:
- Representasi simultan variabel dan observasi: Biplot secara unik menampilkan baik variabel maupun observasi dalam satu diagram, memungkinkan pemahaman langsung tentang hubungan di antara keduanya. Hal ini berbeda dengan beberapa teknik lain yang mungkin hanya memfokuskan pada satu aspek saja.
- Pengurangan dimensionalitas: Biplot mampu mereduksi data berdimensi tinggi menjadi representasi dua dimensi, sehingga memudahkan interpretasi visual. Teknik ini sangat berguna ketika berhadapan dengan dataset yang kompleks dengan banyak variabel.
- Identifikasi pola dan hubungan: Biplot memfasilitasi identifikasi pola dan hubungan linier antara variabel dan observasi. Arah dan panjang vektor variabel menunjukkan korelasi antara variabel, sementara posisi titik observasi menunjukkan kemiripan antara observasi.
- Interpretasi yang relatif mudah: Dibandingkan dengan beberapa metode statistik multivariat lainnya yang kompleks, biplot menawarkan interpretasi yang relatif mudah dan intuitif, terutama bagi mereka yang tidak memiliki latar belakang statistik yang kuat.
Keterbatasan Biplot
Meskipun memiliki banyak keunggulan, biplot juga memiliki keterbatasan yang perlu dipertimbangkan. Interpretasi biplot dapat menjadi rumit, terutama ketika terdapat banyak variabel atau observasi yang berkorelasi tinggi. Berikut beberapa keterbatasannya:
- Kehilangan informasi: Karena reduksi dimensionalitas, beberapa informasi mungkin hilang dalam proses proyeksi ke ruang dua dimensi. Tingkat kehilangan informasi bergantung pada kompleksitas data dan metode biplot yang digunakan.
- Interpretasi yang ambigu: Dalam beberapa kasus, interpretasi biplot dapat menjadi ambigu, terutama ketika vektor variabel saling berdekatan atau ketika titik observasi berkelompok rapat. Hal ini dapat menyebabkan kesimpulan yang salah jika tidak diinterpretasikan dengan hati-hati.
- Sensitivitas terhadap skala variabel: Biplot sensitif terhadap skala variabel. Variabel dengan skala yang sangat berbeda dapat mendominasi plot, sehingga variabel lain yang penting mungkin tersembunyi.
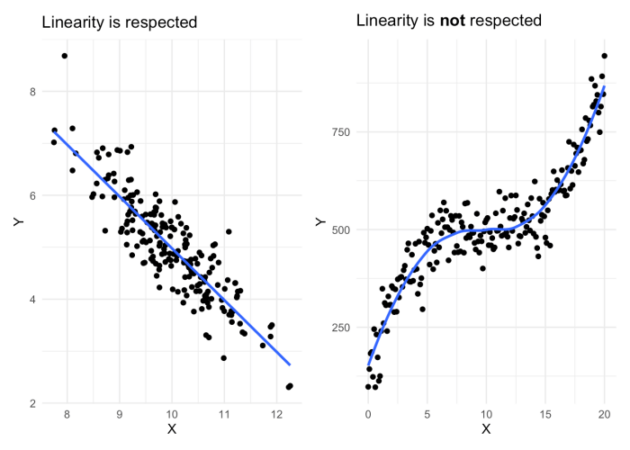
- Asumsi linearitas: Biplot mengasumsikan hubungan linier antara variabel. Jika hubungan antar variabel bersifat non-linier, biplot mungkin tidak memberikan representasi yang akurat.
Contoh Kasus di Mana Biplot Kurang Tepat Digunakan
Sebagai contoh, penggunaan biplot mungkin kurang tepat pada data dengan hubungan non-linier yang kuat antara variabel. Misalnya, dalam menganalisis hubungan antara dosis obat dan respons biologis, jika respons menunjukkan kurva sigmoid (bukan hubungan linier), biplot tidak akan memberikan representasi yang akurat. Dalam kasus seperti ini, teknik visualisasi non-linier mungkin lebih sesuai.
Perbandingan Biplot dengan Teknik Visualisasi Lainnya
Dibandingkan dengan teknik seperti Principal Component Analysis (PCA) plot atau scatter plot biasa, biplot menawarkan keuntungan dengan menampilkan hubungan antara variabel dan observasi secara simultan. PCA plot hanya menampilkan variabel, sementara scatter plot hanya mampu menampilkan dua variabel pada satu waktu. Namun, PCA plot dan scatter plot dapat lebih mudah diinterpretasikan jika data relatif sederhana dan tidak terlalu banyak variabelnya.
Pertimbangan Penggunaan Biplot Berdasarkan Karakteristik Data
Keputusan untuk menggunakan biplot harus didasarkan pada karakteristik data. Biplot paling efektif untuk data dengan jumlah variabel yang moderat dan hubungan linier yang dominan antar variabel. Data dengan banyak variabel yang berkorelasi tinggi atau hubungan non-linier yang kuat mungkin memerlukan teknik visualisasi alternatif.
Aplikasi Biplot dalam Berbagai Bidang
Biplot, sebagai teknik visualisasi data yang handal, menawarkan cara yang efisien untuk menjelajahi hubungan kompleks antar variabel dalam suatu dataset. Kemampuannya dalam menyajikan informasi multidimensi ke dalam representasi dua dimensi membuatnya menjadi alat yang sangat berguna di berbagai disiplin ilmu. Berikut beberapa contoh penerapan biplot yang menunjukkan fleksibilitas dan kekuatannya.
Analisis Data Genomik dalam Biologi
Dalam biologi, khususnya analisis data genomik, biplot digunakan untuk memvisualisasikan hubungan antara gen dan sampel. Misalnya, dalam studi ekspresi gen, biplot dapat menunjukkan gen mana yang diekspresikan secara tinggi atau rendah pada sampel tertentu. Dengan demikian, peneliti dapat mengidentifikasi pola ekspresi gen yang terkait dengan fenotipe atau kondisi tertentu. Visualisasi ini memungkinkan identifikasi gen yang berperan penting dalam suatu proses biologis, mempermudah interpretasi data yang kompleks dan berdimensi tinggi.
Analisis Preferensi Konsumen dalam Penelitian Pasar
Penelitian pasar seringkali melibatkan pengumpulan data tentang preferensi konsumen terhadap berbagai produk atau atribut produk. Biplot sangat berguna dalam menganalisis data ini. Dengan memplot preferensi konsumen dan atribut produk pada diagram yang sama, biplot memungkinkan peneliti untuk mengidentifikasi segmen konsumen yang berbeda berdasarkan preferensi mereka, serta atribut produk yang paling berpengaruh terhadap pilihan konsumen. Contohnya, sebuah perusahaan minuman dapat menggunakan biplot untuk memahami hubungan antara preferensi rasa (manis, asam, pahit) dan demografi konsumen (usia, jenis kelamin), membantu mereka dalam strategi pemasaran yang lebih tertarget.
Analisis Hubungan Polutan dan Faktor Lingkungan
Dalam analisis lingkungan, biplot dapat digunakan untuk memvisualisasikan hubungan antara berbagai polutan dan faktor lingkungan lainnya seperti suhu, kelembaban, dan curah hujan. Dengan memplot variabel-variabel ini pada diagram biplot, peneliti dapat mengidentifikasi pola hubungan antara polutan dan faktor lingkungan, membantu dalam memahami sumber polusi dan dampaknya terhadap lingkungan. Misalnya, biplot dapat menunjukkan hubungan antara konsentrasi logam berat di air sungai dengan tingkat pH dan suhu air, yang membantu dalam menentukan sumber pencemaran dan strategi mitigasi yang tepat.
Analisis Data Survei dalam Ilmu Sosial
Biplot juga bermanfaat dalam ilmu sosial untuk menganalisis data survei yang kompleks. Misalnya, dalam survei kepuasan pelanggan, biplot dapat digunakan untuk memvisualisasikan hubungan antara berbagai aspek kepuasan pelanggan (misalnya, kualitas produk, layanan pelanggan, harga) dan karakteristik demografis responden. Ini memungkinkan peneliti untuk mengidentifikasi kelompok pelanggan dengan karakteristik dan tingkat kepuasan yang berbeda, membantu dalam pengembangan strategi peningkatan kepuasan pelanggan yang lebih efektif.
Dengan demikian, perusahaan dapat lebih memahami kebutuhan dan harapan pelanggan yang berbeda, dan menyesuaikan strategi mereka.
Daftar Aplikasi Biplot di Berbagai Disiplin Ilmu
- Agronomi: Menganalisis hubungan antara sifat tanaman dan kondisi lingkungan.
- Ekonomi: Memvisualisasikan hubungan antara variabel ekonomi makro.
- Kedokteran: Menganalisis hubungan antara biomarker dan hasil kesehatan.
- Psikologi: Menganalisis hubungan antara variabel kepribadian dan perilaku.
- Ekologi: Menganalisis hubungan antara spesies dan habitat.
Penutup

Analisis biplot terbukti menjadi alat yang berharga dalam visualisasi dan interpretasi data multivariat. Kemampuannya untuk menampilkan hubungan antar variabel dan observasi secara simultan memberikan wawasan yang mendalam dan memudahkan pengambilan kesimpulan. Meskipun memiliki beberapa keterbatasan, pemahaman yang baik tentang kekuatan dan kelemahan biplot, serta pemilihan metode yang tepat, akan memastikan penerapan yang efektif dalam berbagai bidang ilmu pengetahuan dan praktis.
Kemampuan untuk mengoptimalkan tampilan biplot, memilih skala yang tepat, dan memahami interpretasi vektor dan titik observasi menjadi kunci dalam memaksimalkan manfaat dari teknik visualisasi data yang efisien ini.