- Jenis Soal Trigonometri Kelas 10
- Rumus dan Konsep Dasar Trigonometri
-
Contoh Soal dan Penyelesaiannya: Contoh Soal Trigonometri Kelas 10
- Contoh Soal Trigonometri dan Penyelesaiannya
- Penyelesaian Soal 1: Nilai sin 30° + cos 60°
- Penyelesaian Soal 2: Nilai tan 45° – cot 45°
- Penyelesaian Soal 3: Menentukan cos x dan tan x
- Penyelesaian Soal 4: Persamaan Trigonometri sin x = 1/2
- Penyelesaian Soal 5: Tinggi Dinding yang Dicapai Tangga
- Kesalahan Umum dan Solusinya
- Penggunaan Kalkulator
- Penerapan Trigonometri dalam Kehidupan Sehari-hari
- Ulasan Penutup
Contoh Soal Trigonometri Kelas 10: Mempelajari trigonometri mungkin terasa menantang, namun dengan latihan soal yang tepat, pemahaman konsep akan semakin terasah. Materi ini mencakup berbagai jenis soal, mulai dari perbandingan trigonometri sudut istimewa hingga penyelesaian persamaan trigonometri yang lebih kompleks. Artikel ini menyajikan beragam contoh soal dengan tingkat kesulitan berbeda, dilengkapi langkah-langkah penyelesaian yang detail, sehingga membantu siswa kelas 10 menguasai materi trigonometri dengan lebih baik.
Dari rumus dasar hingga penerapannya dalam kehidupan sehari-hari, kita akan menjelajahi dunia trigonometri secara komprehensif. Dengan memahami konsep dasar seperti perbandingan trigonometri pada segitiga siku-siku dan identitas trigonometri, siswa akan mampu menyelesaikan berbagai macam soal dengan percaya diri. Soal-soal yang disajikan dalam artikel ini dirancang untuk membantu siswa mengidentifikasi dan mengatasi kesalahan umum yang sering terjadi.
Jenis Soal Trigonometri Kelas 10

Trigonometri di kelas 10 merupakan fondasi penting untuk memahami konsep matematika lanjutan. Materi ini mencakup berbagai jenis soal yang menguji pemahaman siswa terhadap perbandingan trigonometri, identitas trigonometri, dan penyelesaian persamaan trigonometri. Memahami perbedaan dan persamaan antar jenis soal ini sangat krusial untuk menguasai materi trigonometri secara menyeluruh.
Perbandingan Trigonometri Sudut Istimewa
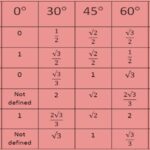
Soal perbandingan trigonometri sudut istimewa fokus pada nilai-nilai sinus, cosinus, dan tangen untuk sudut-sudut tertentu seperti 0°, 30°, 45°, 60°, dan 90°. Pemahaman nilai-nilai ini merupakan dasar untuk menyelesaikan soal trigonometri yang lebih kompleks.
| Jenis Soal | Rumus | Contoh Soal Mudah | Contoh Soal Sedang |
|---|---|---|---|
| Menentukan nilai perbandingan trigonometri sudut istimewa | sin 30° = 1/2, cos 60° = 1/2, tan 45° = 1, dst. | Tentukan nilai sin 30°! | Hitunglah nilai dari 2sin 60° + cos 30° |
Penyelesaian Contoh Soal Mudah: Nilai sin 30° adalah 1/2.
Penyelesaian Contoh Soal Sedang: 2sin 60° + cos 30° = 2(√3/2) + (√3/2) = (3√3)/2
Contoh Soal Sulit: Tentukan nilai dari (sin 45° cos 30°) / tan 60° tanpa menggunakan kalkulator.
Penyelesaian Contoh Soal Sulit: (√2/2)(√3/2) / √3 = √2/4
Identitas Trigonometri
Identitas trigonometri merupakan persamaan yang selalu benar untuk setiap nilai sudut. Menguasai identitas ini penting untuk menyederhanakan ekspresi trigonometri dan menyelesaikan persamaan trigonometri.
| Jenis Soal | Rumus | Contoh Soal Mudah | Contoh Soal Sedang |
|---|---|---|---|
| Membuktikan identitas trigonometri | sin²x + cos²x = 1, tan x = sin x / cos x, dst. | Buktikan bahwa sin²x + cos²x = 1 | Sederhanakan ekspresi: (1 + tan²x)cos²x |
Penyelesaian Contoh Soal Mudah: Bukti identitas sin²x + cos²x = 1 dapat dilakukan dengan menggunakan teorema Pythagoras pada segitiga siku-siku.
Penyelesaian Contoh Soal Sedang: (1 + tan²x)cos²x = (1 + sin²x/cos²x)cos²x = cos²x + sin²x = 1
Contoh Soal Sulit: Buktikan identitas: (tan x + cot x) / (sec x cosec x) = sin 2x
Penyelesaian Contoh Soal Sulit: Bukti ini membutuhkan manipulasi aljabar dan penggunaan beberapa identitas trigonometri dasar.
Penyelesaian Persamaan Trigonometri
Penyelesaian persamaan trigonometri melibatkan pencarian nilai sudut yang memenuhi persamaan trigonometri tertentu. Jenis soal ini membutuhkan pemahaman yang baik tentang identitas trigonometri dan sifat-sifat periodik fungsi trigonometri.
| Jenis Soal | Rumus | Contoh Soal Mudah | Contoh Soal Sedang |
|---|---|---|---|
| Mencari nilai x yang memenuhi persamaan trigonometri | Bergantung pada persamaan, misalnya sin x = 1/2, cos x = -1, dst. | Tentukan nilai x yang memenuhi sin x = 1/2 untuk 0° ≤ x ≤ 360° | Tentukan nilai x yang memenuhi 2cos²x – 1 = 0 untuk 0° ≤ x ≤ 360° |
Penyelesaian Contoh Soal Mudah: x = 30° dan x = 150°
Penyelesaian Contoh Soal Sedang: cos²x = 1/2 => cos x = ±1/√2. Oleh karena itu, x = 45°, 135°, 225°, 315°.
Contoh Soal Sulit: Tentukan himpunan penyelesaian dari persamaan 2sin²x + 3cosx – 3 = 0 untuk 0 ≤ x ≤ 2π.
Penyelesaian Contoh Soal Sulit: Soal ini membutuhkan penggunaan identitas trigonometri dan metode aljabar untuk menyelesaikan persamaan kuadrat.
Rumus dan Konsep Dasar Trigonometri

Trigonometri merupakan cabang matematika yang mempelajari hubungan antara sudut dan sisi-sisi dalam segitiga. Pemahaman konsep dasar trigonometri sangat penting untuk menyelesaikan berbagai masalah matematika dan fisika, khususnya yang berkaitan dengan geometri dan vektor. Pada tingkat kelas 10, fokus utama adalah pada trigonometri segitiga siku-siku, yang melibatkan perbandingan antara panjang sisi-sisi segitiga tersebut terhadap sudut-sudutnya.
Rumus Dasar Trigonometri Segitiga Siku-Siku
Dalam segitiga siku-siku, terdapat tiga perbandingan trigonometri dasar yang didefinisikan berdasarkan panjang sisi-sisi terhadap sudut lancipnya. Ketiga perbandingan ini adalah sinus (sin), kosinus (cos), dan tangen (tan). Rumus-rumus ini menjadi fondasi untuk memahami dan menyelesaikan berbagai soal trigonometri.
- Sinus (sin):
sin θ = sisi depan / sisi miring
. Sisi depan adalah sisi yang berhadapan dengan sudut θ, sedangkan sisi miring adalah sisi terpanjang dalam segitiga siku-siku (sisi yang berhadapan dengan sudut siku-siku). - Kosinus (cos):
cos θ = sisi samping / sisi miring
. Sisi samping adalah sisi yang berdekatan dengan sudut θ, tetapi bukan sisi miring. - Tangen (tan):
tan θ = sisi depan / sisi samping
. Perbandingan ini merupakan hasil bagi antara sinus dan kosinus, yaitutan θ = sin θ / cos θ
.
Ilustrasi Hubungan Sudut dan Perbandingan Trigonometri
Bayangkan sebuah segitiga siku-siku dengan sudut lancip θ. Sisi di depan sudut θ kita sebut sebagai ‘a’, sisi di samping sudut θ sebagai ‘b’, dan sisi miring (hipotenusa) sebagai ‘c’. Ilustrasi ini menggambarkan bagaimana panjang sisi ‘a’, ‘b’, dan ‘c’ berhubungan dengan besar sudut θ melalui perbandingan trigonometri. Semakin besar sudut θ, semakin panjang sisi ‘a’ relatif terhadap sisi ‘b’ dan ‘c’, sehingga nilai sin θ akan meningkat, sementara nilai cos θ akan menurun.
Nilai tan θ akan mencerminkan perubahan rasio antara sisi depan dan sisi samping.
Penerapan Rumus Trigonometri dalam Soal
Misalnya, kita memiliki segitiga siku-siku dengan sisi miring sepanjang 10 cm dan salah satu sudut lancipnya sebesar 30°. Jika kita ingin mencari panjang sisi di depan sudut 30°, kita dapat menggunakan rumus sinus: sin 30° = sisi depan / 10 cm. Karena sin 30° = 0.5, maka panjang sisi depan adalah 10 cm
– 0.5 = 5 cm.
Contoh lain, jika diketahui panjang sisi depan (a) = 5 cm dan sisi samping (b) = 8 cm, kita dapat mencari nilai tangen sudut θ dengan rumus tan θ = 5/8. Dengan menggunakan kalkulator, kita dapat mencari nilai θ (sudut) yang sesuai.
Perbandingan dan Perbedaan Rumus Trigonometri
Ketiga rumus dasar trigonometri (sin, cos, tan) saling berkaitan. Sinus dan kosinus memiliki penyebut yang sama (sisi miring), sedangkan tangen merupakan perbandingan antara sinus dan kosinus. Perbedaan utama terletak pada sisi-sisi segitiga yang dibandingkan. Sinus membandingkan sisi depan dengan sisi miring, kosinus membandingkan sisi samping dengan sisi miring, dan tangen membandingkan sisi depan dengan sisi samping. Kesamaan di antara ketiganya adalah bahwa semuanya bergantung pada sudut dalam segitiga siku-siku dan memberikan informasi tentang rasio panjang sisi-sisi segitiga tersebut.
Contoh Soal dan Penyelesaiannya: Contoh Soal Trigonometri Kelas 10
Trigonometri merupakan cabang matematika yang mempelajari hubungan antara sudut dan sisi-sisi dalam segitiga. Pemahaman yang kuat tentang konsep dasar trigonometri sangat penting untuk menyelesaikan berbagai permasalahan, baik dalam matematika lanjut maupun aplikasi di bidang lain seperti fisika dan teknik. Berikut beberapa contoh soal trigonometri kelas 10 dengan tingkat kesulitan bervariasi, disertai penyelesaian langkah demi langkah dan penjelasan konsep kunci.
Contoh Soal Trigonometri dan Penyelesaiannya
Berikut lima contoh soal trigonometri beserta penyelesaiannya. Soal-soal ini dirancang untuk menguji pemahaman berbagai konsep dasar trigonometri, mulai dari nilai trigonometri sudut istimewa hingga penerapan rumus-rumus trigonometri.
- Soal 1: Tentukan nilai dari sin 30° + cos 60°.
- Soal 2: Hitunglah nilai tan 45° – cot 45°.
- Soal 3: Jika sin x = 3/5 dan x sudut lancip, tentukan nilai cos x dan tan x.
- Soal 4: Selesaikan persamaan trigonometri sin x = 1/2 untuk 0° ≤ x ≤ 360°.
- Soal 5: Sebuah tangga sepanjang 5 meter bersandar pada dinding. Jika sudut yang dibentuk tangga dengan tanah adalah 60°, tentukan tinggi dinding yang dicapai tangga.
Penyelesaian Soal 1: Nilai sin 30° + cos 60°
Untuk menyelesaikan soal ini, kita perlu mengingat nilai trigonometri sudut istimewa. Nilai sin 30° adalah 1/2 dan nilai cos 60° juga 1/
2. Oleh karena itu:
sin 30° + cos 60° = 1/2 + 1/2 = 1
Penyelesaian Soal 2: Nilai tan 45° – cot 45°
Sama seperti soal sebelumnya, kita perlu mengingat nilai trigonometri sudut istimewa. Nilai tan 45° adalah 1 dan nilai cot 45° juga
1. Maka:
tan 45°
cot 45° = 1 – 1 = 0
Penyelesaian Soal 3: Menentukan cos x dan tan x
Diketahui sin x = 3/
5. Karena x sudut lancip, kita dapat menggunakan identitas trigonometri sin²x + cos²x = 1 untuk mencari nilai cos x. Substitusikan sin x = 3/5:
(3/5)² + cos²x = 1 => cos²x = 1 – 9/25 = 16/25 => cos x = ±4/5
Karena x sudut lancip, maka cos x = 4/
5. Selanjutnya, kita dapat mencari tan x menggunakan rumus tan x = sin x / cos x:
tan x = (3/5) / (4/5) = 3/4
Penyelesaian Soal 4: Persamaan Trigonometri sin x = 1/2
Persamaan sin x = 1/2 memiliki dua solusi dalam rentang 0° ≤ x ≤ 360°. Solusi pertama adalah x = 30° (sudut istimewa). Solusi kedua berada di kuadran II, yaitu 180°
-30° = 150°.
Oleh karena itu, solusi dari persamaan sin x = 1/2 adalah x = 30° dan x = 150°.
Penyelesaian Soal 5: Tinggi Dinding yang Dicapai Tangga
Soal ini melibatkan penerapan trigonometri dalam konteks geometri. Kita dapat menggunakan fungsi trigonometri sinus untuk menyelesaikannya. Misalkan h adalah tinggi dinding yang dicapai tangga. Maka:
sin 60° = h / 5 => h = 5 sin 60° = 5 (√3/2) ≈ 4.33 meter
Kesalahan Umum dan Solusinya
Kesalahan umum yang sering dilakukan siswa dalam menyelesaikan soal trigonometri antara lain: keliru dalam mengingat nilai trigonometri sudut istimewa, salah menggunakan identitas trigonometri, dan kesulitan dalam memahami konsep sudut di berbagai kuadran. Solusinya adalah dengan rajin berlatih mengerjakan soal, memahami konsep dasar dengan baik, dan menggunakan kalkulator secara tepat.
Penggunaan Kalkulator
Untuk soal trigonometri yang kompleks, kalkulator sangat membantu. Pastikan kalkulator diatur dalam mode derajat (°) jika sudut dinyatakan dalam derajat, atau radian (rad) jika sudut dinyatakan dalam radian. Ketelitian dalam memasukkan nilai dan memilih fungsi trigonometri yang tepat sangat penting untuk mendapatkan hasil yang akurat.
Penerapan Trigonometri dalam Kehidupan Sehari-hari
Trigonometri, cabang matematika yang mempelajari hubungan antara sudut dan sisi segitiga, ternyata memiliki penerapan yang luas dalam kehidupan sehari-hari. Meskipun mungkin tidak terlihat secara langsung, prinsip-prinsip trigonometri berperan penting dalam berbagai bidang, dari arsitektur hingga navigasi. Berikut beberapa contoh penerapannya.
Pengukuran Tinggi Bangunan
Trigonometri sangat berguna dalam menentukan tinggi bangunan atau objek yang sulit diukur secara langsung. Dengan menggunakan alat ukur sudut (seperti teodolit) dan mengukur jarak dari titik pengamatan ke dasar bangunan, kita dapat menggunakan fungsi trigonometri, khususnya tangen, untuk menghitung tinggi bangunan.
Misalnya, jika kita berdiri sejauh 30 meter dari sebuah gedung dan mengukur sudut elevasi puncak gedung sebesar 60 derajat, kita dapat menggunakan rumus tan(60°) = tinggi gedung / 30 meter. Dengan mengetahui nilai tan(60°) = √3, kita dapat menghitung tinggi gedung tersebut.
Ilustrasi: Bayangkan sebuah segitiga siku-siku. Sisi miring mewakili jarak pandang ke puncak gedung (garis pandang), sisi tegak mewakili tinggi gedung yang ingin diukur, dan sisi mendatar mewakili jarak pengamat dari dasar gedung. Sudut elevasi adalah sudut yang dibentuk oleh garis horizontal dan garis pandang ke puncak gedung.
Navigasi dan Pemetaan, Contoh soal trigonometri kelas 10
Dalam navigasi, trigonometri digunakan untuk menentukan posisi dan arah. Sistem navigasi berbasis GPS, misalnya, memanfaatkan trigonometri untuk menghitung jarak dan posisi relatif antara satelit dan penerima GPS di permukaan bumi.
Penerapan lain dalam pemetaan adalah pembuatan peta topografi. Trigonometri digunakan untuk menghitung ketinggian titik-titik di permukaan bumi berdasarkan pengukuran sudut dan jarak. Dengan data ini, peta yang akurat dapat dibuat untuk menunjukkan kontur permukaan tanah.
Ilustrasi: Bayangkan sebuah kapal di laut. Kapten kapal menggunakan GPS untuk menentukan koordinat posisinya. Sistem GPS menggunakan prinsip-prinsip trigonometri untuk menghitung jarak antara satelit dan kapal, kemudian menentukan posisi kapal berdasarkan perpotongan beberapa jarak tersebut.
Desain dan Konstruksi
Dalam bidang arsitektur dan konstruksi, trigonometri digunakan untuk perhitungan sudut, kemiringan, dan panjang dalam berbagai struktur. Misalnya, dalam pembangunan jembatan, trigonometri digunakan untuk menghitung panjang kabel penyangga dan sudut kemiringan struktur agar kuat dan stabil.
Contoh lain adalah dalam desain atap rumah. Trigonometri digunakan untuk menghitung sudut kemiringan atap, panjang kasau, dan ukuran lainnya agar atap dapat menahan beban dan berfungsi dengan baik.
Ilustrasi: Perhatikan sebuah jembatan gantung. Kabel-kabel penyangga jembatan membentuk segitiga dengan tiang penyangga dan dek jembatan. Trigonometri digunakan untuk menghitung panjang dan tegangan kabel agar jembatan dapat menahan beban lalu lintas.
Keterbatasan Penggunaan Trigonometri
Meskipun bermanfaat, trigonometri memiliki keterbatasan. Akurasi hasil perhitungan trigonometri bergantung pada akurasi pengukuran awal (sudut dan jarak). Kesalahan kecil dalam pengukuran dapat mengakibatkan kesalahan yang signifikan dalam hasil perhitungan, terutama jika melibatkan beberapa perhitungan berturut-turut. Selain itu, trigonometri planar (pada bidang datar) tidak dapat langsung diterapkan pada permukaan bumi yang bulat tanpa mempertimbangkan kurvatur bumi, sehingga perlu metode lain yang lebih kompleks untuk perhitungan jarak dan posisi yang akurat dalam skala besar.
Skenario Penerapan Trigonometri
Seorang surveyor ingin mengukur lebar sungai tanpa harus menyeberanginya. Ia dapat mengukur jarak dari titik A ke titik B di satu sisi sungai, kemudian mengukur sudut antara titik A, titik B, dan titik C di seberang sungai (titik C berada tepat di seberang titik B). Dengan menggunakan aturan sinus atau cosinus, surveyor dapat menghitung lebar sungai (jarak antara titik B dan C).
Ulasan Penutup
Trigonometri, meskipun terlihat rumit pada awalnya, sebenarnya merupakan cabang matematika yang sangat berguna dan memiliki banyak aplikasi dalam kehidupan nyata. Dengan memahami konsep dasar dan berlatih menyelesaikan berbagai jenis soal, siswa kelas 10 akan mampu menguasai trigonometri dan menerapkannya dalam berbagai konteks. Semoga contoh soal dan penjelasan yang diberikan dalam artikel ini bermanfaat dalam membantu siswa mencapai pemahaman yang lebih baik dan meningkatkan kemampuan pemecahan masalah dalam trigonometri.
