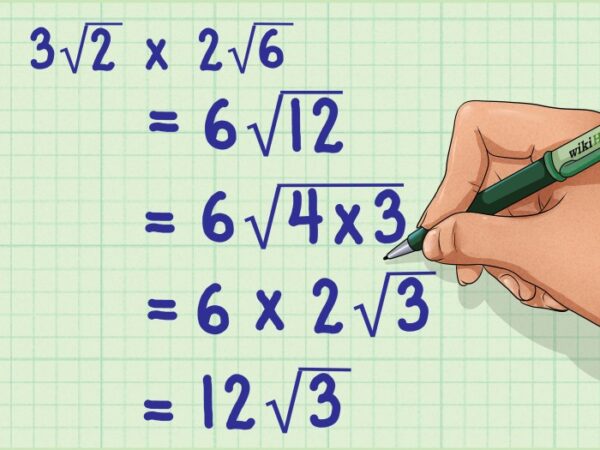
Tabel akar pangkat 2 – Tabel akar pangkat dua merupakan alat yang sangat berguna dalam berbagai bidang, mulai dari matematika dasar hingga aplikasi teknik yang kompleks. Memahami konsep akar pangkat dua dan cara menghitungnya merupakan kunci untuk menguasai berbagai rumus dan persamaan matematika. Artikel ini akan membahas secara rinci tentang pengertian akar pangkat dua, metode perhitungannya, penerapannya dalam kehidupan sehari-hari, serta sifat-sifatnya yang penting.
Kita akan menjelajahi berbagai metode perhitungan, mulai dari metode sederhana hingga penggunaan kalkulator, serta mengkaji penerapannya dalam berbagai konteks.
Dari definisi akar pangkat dua hingga penerapannya dalam geometri dan fisika, kita akan mengupas tuntas topik ini dengan contoh-contoh yang mudah dipahami. Dengan pemahaman yang komprehensif, Anda akan mampu menyelesaikan berbagai permasalahan yang melibatkan akar pangkat dua dengan percaya diri.
Pengertian Akar Pangkat Dua

Akar pangkat dua merupakan konsep dasar dalam matematika yang berkaitan dengan operasi kebalikan dari pangkat dua. Secara sederhana, akar pangkat dua suatu bilangan adalah bilangan yang jika dikuadratkan (dikalikan dengan dirinya sendiri) akan menghasilkan bilangan tersebut. Konsep ini sangat penting dalam berbagai bidang, mulai dari geometri hingga fisika.
Secara matematis, akar pangkat dua dari suatu bilangan x dinotasikan sebagai √ x atau x1/2. Jadi, jika y = √ x, maka y2 = x. Hal ini berarti y dikalikan dengan dirinya sendiri sama dengan x.
Contoh Perhitungan Akar Pangkat Dua
Berikut beberapa contoh perhitungan akar pangkat dua dari beberapa bilangan bulat positif:
- √9 = 3, karena 3 x 3 = 9
- √16 = 4, karena 4 x 4 = 16
- √25 = 5, karena 5 x 5 = 25
- √100 = 10, karena 10 x 10 = 100
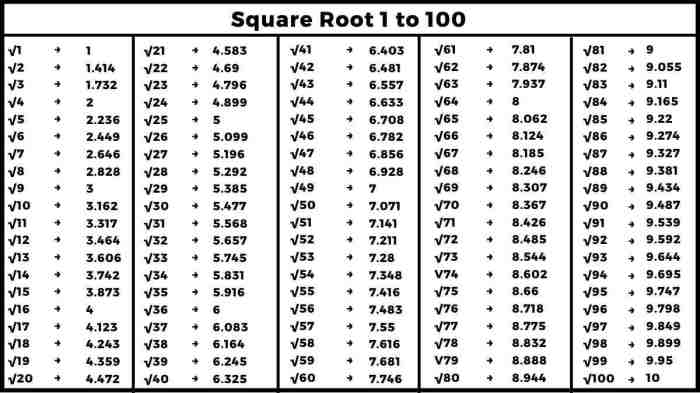
Tabel Akar Pangkat Dua Bilangan 1 sampai 10
Tabel berikut menunjukkan bilangan bulat dari 1 sampai 10 dan akar pangkat duanya. Perhatikan bahwa akar pangkat dua dari beberapa bilangan, seperti 2, 3, 5, 7, dan lain-lain, menghasilkan bilangan desimal yang tidak berulang (irasional).
| Bilangan | Akar Pangkat Dua |
|---|---|
| 1 | 1 |
| 2 | 1.414 |
| 3 | 1.732 |
| 4 | 2 |
| 5 | 2.236 |
| 6 | 2.449 |
| 7 | 2.646 |
| 8 | 2.828 |
| 9 | 3 |
| 10 | 3.162 |
Perbandingan Akar Pangkat Dua dan Pangkat Dua
Akar pangkat dua dan pangkat dua merupakan operasi yang saling berlawanan. Pangkat dua suatu bilangan berarti mengalikan bilangan tersebut dengan dirinya sendiri, sedangkan akar pangkat dua mencari bilangan yang jika dikuadratkan akan menghasilkan bilangan awal. Contohnya, 5 2 = 25, dan √25 = 5.
Contoh Soal Cerita yang Melibatkan Akar Pangkat Dua
Sebuah taman berbentuk bujursangkar memiliki luas 144 meter persegi. Berapa panjang sisi taman tersebut? Untuk menyelesaikan soal ini, kita perlu mencari akar pangkat dua dari luas taman, yaitu √144 = 12 meter. Jadi, panjang sisi taman tersebut adalah 12 meter.
Metode Perhitungan Akar Pangkat Dua
Mencari akar pangkat dua suatu bilangan dapat dilakukan melalui beberapa metode, masing-masing dengan tingkat efisiensi dan kompleksitas yang berbeda. Pemilihan metode yang tepat bergantung pada kebutuhan dan sumber daya yang tersedia. Berikut ini akan diuraikan beberapa metode perhitungan akar pangkat dua, beserta contoh penerapan dan perbandingan efisiensi.
Metode Bagi Dua
Metode bagi dua merupakan metode iteratif yang sederhana untuk memperkirakan akar pangkat dua. Metode ini bekerja dengan secara berulang-ulang mempersempit rentang nilai yang mungkin menjadi akar pangkat dua hingga mencapai tingkat akurasi yang diinginkan. Cara kerjanya adalah dengan mengambil titik tengah dari rentang tersebut dan mengevaluasi apakah titik tengah tersebut merupakan akar pangkat dua yang dicari. Jika tidak, rentang pencarian akan dipersempit menjadi setengahnya, bergantung pada apakah titik tengah tersebut lebih besar atau lebih kecil dari akar pangkat dua yang sebenarnya.
Berikut contoh perhitungan akar pangkat dua dari 25 menggunakan metode bagi dua:
- Tentukan rentang awal. Misalnya, kita mulai dengan rentang [0, 25].
- Hitung titik tengah rentang: (0 + 25) / 2 = 12.5
- Kuadratkan titik tengah: 12.5² = 156.25. Karena ini lebih besar dari 25, akarnya berada di antara 0 dan 12.5.
- Persempit rentang menjadi [0, 12.5]. Titik tengah baru: (0 + 12.5) / 2 = 6.25
- Kuadratkan titik tengah: 6.25² = 39.0625. Masih lebih besar dari 25, jadi rentang menjadi [0, 6.25].
- Ulangi proses ini hingga mencapai tingkat akurasi yang diinginkan. Setelah beberapa iterasi, kita akan mendekati nilai 5.
Metode Iterasi Newton-Raphson
Metode Newton-Raphson merupakan metode iteratif yang lebih efisien dibandingkan metode bagi dua. Metode ini menggunakan turunan fungsi untuk memperkirakan akar pangkat dua dengan lebih cepat. Rumus iterasinya adalah x n+1 = 0.5
– (x n + a / x n), di mana ‘a’ adalah bilangan yang akar pangkat duanya dicari, dan x n adalah perkiraan akar pada iterasi ke-n.
Proses ini diulang hingga mencapai tingkat konvergensi yang diinginkan.
Penggunaan Kalkulator
Metode paling sederhana dan efisien untuk menghitung akar pangkat dua adalah dengan menggunakan kalkulator. Kalkulator, baik fisik maupun digital, umumnya memiliki tombol khusus untuk menghitung akar pangkat dua.
- Masukkan bilangan yang akar pangkat duanya ingin dicari.
- Tekan tombol akar pangkat dua (biasanya ditandai dengan simbol √).
- Hasil perhitungan akan ditampilkan.
Perbandingan Efisiensi Metode, Tabel akar pangkat 2
Metode Newton-Raphson umumnya lebih efisien daripada metode bagi dua karena konvergensi yang lebih cepat. Penggunaan kalkulator merupakan metode yang paling efisien karena perhitungan dilakukan secara langsung oleh perangkat keras atau perangkat lunak kalkulator. Metode bagi dua, meskipun sederhana, membutuhkan lebih banyak iterasi untuk mencapai tingkat akurasi yang sama dibandingkan dengan metode Newton-Raphson.
Penerapan Akar Pangkat Dua

Akar pangkat dua, meskipun tampak sederhana, memiliki penerapan yang luas dan mendalam dalam berbagai bidang ilmu dan kehidupan sehari-hari. Konsep ini tidak hanya terbatas pada perhitungan matematika dasar, tetapi juga menjadi fondasi dalam pemecahan masalah di bidang geometri, fisika, teknik, dan bahkan ilmu-ilmu lainnya.
Penerapan Akar Pangkat Dua dalam Geometri
Dalam geometri, akar pangkat dua sering digunakan untuk menghitung panjang sisi atau diagonal suatu bangun datar. Salah satu contoh yang paling umum adalah perhitungan panjang diagonal persegi. Jika kita memiliki persegi dengan panjang sisi s, maka panjang diagonalnya ( d) dapat dihitung menggunakan teorema Pythagoras: d = √(s² + s²) = s√2. Rumus ini menunjukkan bahwa akar pangkat dua diperlukan untuk menentukan panjang diagonal dari panjang sisinya.
Penerapan Akar Pangkat Dua dalam Fisika
Konsep akar pangkat dua juga berperan penting dalam berbagai perhitungan fisika. Misalnya, dalam perhitungan kecepatan, jika kita mengetahui jarak ( s) dan waktu ( t), kecepatan ( v) dapat dihitung dengan rumus v = s/t. Namun, jika kita mengetahui besar kecepatan suatu benda yang bergerak dalam dua arah tegak lurus, misalnya kecepatan horizontal ( vx) dan kecepatan vertikal ( vy), maka kecepatan total ( v) dapat dihitung menggunakan teorema Pythagoras: v = √(vx² + vy²).
Akar pangkat dua di sini digunakan untuk mendapatkan nilai kecepatan total.
Penerapan Akar Pangkat Dua dalam Teknik
Dalam bidang teknik sipil, akar pangkat dua digunakan dalam perhitungan struktur bangunan. Misalnya, dalam mendesain jembatan atau gedung pencakar langit, perhitungan kekuatan dan stabilitas struktur sering melibatkan perhitungan vektor gaya yang membutuhkan penggunaan akar pangkat dua untuk menghitung resultan gaya. Selain itu, dalam perencanaan jalur pipa atau kabel bawah tanah, perhitungan jarak terpendek antara dua titik seringkali melibatkan penggunaan teorema Pythagoras dan, karenanya, akar pangkat dua.
Penggunaan Akar Pangkat Dua dalam Rumus Matematika Lainnya
Akar pangkat dua merupakan komponen penting dalam berbagai rumus matematika lainnya. Misalnya, dalam rumus kuadrat, ax² + bx + c = 0, akar pangkat dua digunakan dalam rumus penyelesaiannya untuk mencari nilai x: x = (-b ± √(b²
-4ac)) / 2a . Akar pangkat dua juga sering muncul dalam kalkulus, khususnya dalam perhitungan turunan dan integral fungsi-fungsi tertentu. Contoh lain adalah dalam perhitungan jarak antara dua titik dalam koordinat kartesius tiga dimensi yang melibatkan rumus jarak yang menggunakan akar pangkat dua.
Sifat-Sifat Akar Pangkat Dua
Akar pangkat dua, atau sering ditulis sebagai √, merupakan operasi matematika yang mencari bilangan yang jika dikuadratkan (dikalikan dengan dirinya sendiri) menghasilkan bilangan di dalam tanda akar. Memahami sifat-sifat akar pangkat dua sangat penting untuk mempermudah perhitungan dan pemecahan masalah matematika, terutama dalam aljabar dan geometri.
Beberapa sifat penting akar pangkat dua akan dijelaskan berikut ini, disertai contoh dan ilustrasi untuk memperjelas pemahaman.
Sifat-Sifat Akar Pangkat Dua dan Contohnya
Berikut ini beberapa sifat penting akar pangkat dua yang perlu dipahami. Pemahaman sifat-sifat ini akan membantu dalam menyelesaikan berbagai soal yang melibatkan akar pangkat dua dengan lebih efisien dan akurat.
| Sifat | Penjelasan | Contoh | Ilustrasi |
|---|---|---|---|
| √(a x b) = √a x √b (untuk a dan b ≥ 0) | Akar pangkat dua dari perkalian dua bilangan non-negatif sama dengan perkalian akar pangkat dua dari masing-masing bilangan. | √(9 x 4) = √9 x √4 = 3 x 2 = 6 | Ilustrasi: Bayangkan sebuah persegi panjang dengan luas 36 satuan luas. Jika kita bagi persegi panjang tersebut menjadi dua persegi dengan luas 9 dan 4 satuan luas, maka panjang sisi persegi pertama adalah √9 = 3 dan sisi persegi kedua adalah √4 = 2. Panjang sisi persegi yang luasnya 36 adalah √36 = 6, yang sama dengan 3 + 2. Ini menunjukkan bahwa √(9 x 4) = √9 x √4. |
| √(a/b) = √a / √b (untuk a ≥ 0 dan b > 0) | Akar pangkat dua dari hasil bagi dua bilangan (pembilang non-negatif dan penyebut positif) sama dengan hasil bagi akar pangkat dua dari masing-masing bilangan. | √(16/4) = √16 / √4 = 4 / 2 = 2 | Ilustrasi: Bayangkan sebuah persegi dengan luas 16 satuan luas yang dibagi menjadi 4 persegi kecil yang sama. Luas setiap persegi kecil adalah 16/4 = 4 satuan luas. Panjang sisi persegi besar adalah √16 = 4, dan panjang sisi persegi kecil adalah √4 = 2. Perbandingan panjang sisi persegi besar dan kecil adalah 4/2 = 2, yang sama dengan √(16/4). |
| (√a)² = a (untuk a ≥ 0) | Kuadrat dari akar pangkat dua suatu bilangan non-negatif sama dengan bilangan itu sendiri. | (√25)² = 25 | Ilustrasi: Jika kita memiliki sebuah persegi dengan panjang sisi √25 = 5, maka luas persegi tersebut adalah 5² = 25 satuan luas. Ini menunjukkan bahwa mengkuadratkan akar pangkat dua suatu bilangan akan mengembalikan bilangan tersebut. |
| √a² = |a| | Akar pangkat dua dari kuadrat suatu bilangan sama dengan nilai absolut bilangan tersebut. | √(-3)² = |-3| = 3 | Ilustrasi: Nilai absolut memastikan hasil selalu non-negatif. Kuadrat dari -3 adalah 9, dan akar pangkat dua dari 9 adalah 3 (bukan -3). Nilai absolut menjamin hasil yang konsisten. |
Penerapan Sifat Akar Pangkat Dua dalam Pemecahan Masalah
Sifat-sifat akar pangkat dua di atas sangat berguna dalam menyederhanakan ekspresi aljabar yang kompleks dan mempercepat proses perhitungan. Misalnya, dalam menyelesaikan persamaan kuadrat, memahami sifat-sifat ini membantu dalam mencari akar-akar persamaan tersebut. Selain itu, sifat-sifat ini juga krusial dalam geometri, terutama dalam penerapan Teorema Pythagoras.
Hubungan Akar Pangkat Dua dan Teorema Pythagoras
Teorema Pythagoras menyatakan bahwa dalam segitiga siku-siku, kuadrat panjang sisi miring (hipotenusa) sama dengan jumlah kuadrat panjang kedua sisi lainnya (sisi tegak). Rumusnya adalah a² + b² = c², di mana a dan b adalah panjang sisi tegak, dan c adalah panjang sisi miring. Untuk mencari panjang sisi miring, kita perlu menghitung akar pangkat dua dari jumlah kuadrat sisi tegak (c = √(a² + b²)).
Begitu pula, jika kita mengetahui panjang sisi miring dan salah satu sisi tegak, kita dapat menggunakan akar pangkat dua untuk menghitung panjang sisi tegak lainnya.
Sebagai contoh, jika sebuah segitiga siku-siku memiliki sisi tegak sepanjang 3 dan 4 satuan, maka panjang sisi miringnya adalah √(3² + 4²) = √(9 + 16) = √25 = 5 satuan. Dalam kasus ini, akar pangkat dua digunakan secara langsung untuk menghitung panjang sisi miring berdasarkan Teorema Pythagoras.
Akar Pangkat Dua dari Bilangan Desimal dan Pecahan
Menghitung akar pangkat dua dari bilangan bulat relatif mudah. Namun, bagaimana jika bilangan yang ingin kita cari akar pangkat duanya berupa bilangan desimal atau pecahan? Prosesnya sedikit berbeda, tetapi tetap dapat dikerjakan dengan metode dan pemahaman yang tepat. Berikut penjelasan lebih lanjut mengenai perhitungan akar pangkat dua untuk bilangan desimal dan pecahan.
Pada dasarnya, menghitung akar pangkat dua dari bilangan desimal dan pecahan melibatkan prinsip yang sama dengan bilangan bulat, yaitu mencari bilangan yang jika dikuadratkan (dikalikan dengan dirinya sendiri) menghasilkan bilangan asal. Perbedaannya terletak pada penanganan koma desimal dan penyederhanaan pecahan. Untuk bilangan desimal, kita dapat menggunakan kalkulator atau metode iteratif seperti metode Newton-Raphson untuk mendapatkan aproksimasi akar pangkat dua.
Sedangkan untuk pecahan, kita dapat mencari akar pangkat dua dari pembilang dan penyebut secara terpisah.
Perhitungan Akar Pangkat Dua Bilangan Desimal
Menghitung akar pangkat dua bilangan desimal dapat dilakukan dengan beberapa cara. Cara termudah adalah menggunakan kalkulator. Namun, untuk memahami prosesnya, kita dapat menggunakan pendekatan aproksimasi. Misalnya, untuk mencari akar pangkat dua dari 2.25, kita dapat menebak nilai awal, lalu mengulang proses perhitungan sampai mencapai tingkat akurasi yang diinginkan. Atau, kita bisa mengubah bilangan desimal menjadi pecahan terlebih dahulu, lalu menghitung akar pangkat dua dari pecahan tersebut.
Contoh: Akar pangkat dua dari 2.25. Kita tahu bahwa 1.5 x 1.5 = 2.25, sehingga akar pangkat dua dari 2.25 adalah 1.5.
Contoh lain: Akar pangkat dua dari 12.96. Dengan kalkulator, kita dapat langsung memperoleh hasilnya yaitu 3.6.
Perhitungan Akar Pangkat Dua Bilangan Pecahan
Mencari akar pangkat dua dari bilangan pecahan melibatkan mencari akar pangkat dua dari pembilang dan penyebut secara terpisah. Misalnya, untuk mencari akar pangkat dua dari pecahan 9/25, kita mencari akar pangkat dua dari 9 (yaitu 3) dan akar pangkat dua dari 25 (yaitu 5). Hasilnya adalah 3/5.
Contoh: Akar pangkat dua dari 49/100. Akar pangkat dua dari 49 adalah 7, dan akar pangkat dua dari 100 adalah 10. Jadi, akar pangkat dua dari 49/100 adalah 7/10 atau 0.7.
Namun, tidak semua pecahan memiliki akar pangkat dua yang berupa pecahan sederhana. Dalam kasus seperti ini, kita mungkin perlu menggunakan kalkulator atau metode numerik untuk mendapatkan aproksimasi.
Contoh Soal dan Penyelesaian
Hitunglah akar pangkat dua dari 0.64 dan 25/49.
- Untuk 0.64, kita dapat mengubahnya menjadi pecahan 64/100. Akar pangkat dua dari 64 adalah 8, dan akar pangkat dua dari 100 adalah 10. Jadi, akar pangkat dua dari 0.64 adalah 8/10 atau 0.8.
- Untuk 25/49, akar pangkat dua dari 25 adalah 5, dan akar pangkat dua dari 49 adalah 7. Jadi, akar pangkat dua dari 25/49 adalah 5/7.
Tabel Perbandingan Perhitungan Akar Pangkat Dua
Tabel berikut membandingkan perhitungan akar pangkat dua untuk bilangan bulat, desimal, dan pecahan.
| Bilangan | Jenis Bilangan | Akar Pangkat Dua | Metode Perhitungan |
|---|---|---|---|
| 16 | Bulat | 4 | Faktorisasi prima atau kalkulator |
| 2.25 | Desimal | 1.5 | Kalkulator atau konversi ke pecahan |
| 9/16 | Pecahan | 3/4 | Mencari akar pangkat dua pembilang dan penyebut |
| 0.81 | Desimal | 0.9 | Kalkulator atau konversi ke pecahan |
Penutupan: Tabel Akar Pangkat 2
Memahami akar pangkat dua bukan hanya tentang menghafal rumus, tetapi juga tentang mengaplikasikan konsep tersebut dalam berbagai situasi. Setelah mempelajari pengertian, metode perhitungan, penerapan, dan sifat-sifat akar pangkat dua, diharapkan Anda kini memiliki pemahaman yang lebih komprehensif dan mampu menyelesaikan berbagai soal yang berkaitan dengan akar pangkat dua. Kemampuan ini akan sangat berguna dalam berbagai bidang studi dan kehidupan sehari-hari.