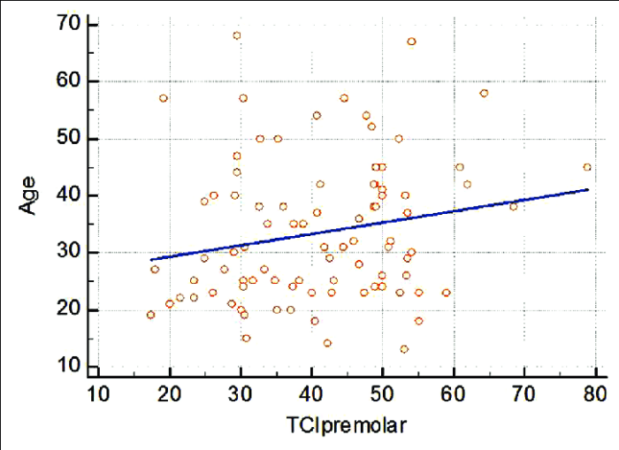
Analisis multivariat merupakan teknik statistik yang ampuh untuk mengungkap pola tersembunyi dalam kumpulan data kompleks yang melibatkan banyak variabel. Bayangkan mencoba memahami perilaku konsumen berdasarkan usia, pendapatan, dan preferensi produk secara bersamaan; analisis multivariat memungkinkan hal tersebut. Teknik ini digunakan luas dalam berbagai bidang, mulai dari pemasaran dan keuangan hingga ilmu kesehatan dan lingkungan, untuk menjawab pertanyaan yang rumit dan membuat keputusan yang lebih baik berdasarkan data.
Dengan mempelajari berbagai metode seperti analisis faktor, analisis klaster, dan analisis diskriminan, kita dapat mereduksi dimensi data, mengelompokkan data serupa, dan bahkan memprediksi kelompok mana yang paling mungkin dimiliki suatu observasi baru. Pemahaman mendalam tentang analisis multivariat memberikan kemampuan untuk melihat gambaran besar dari data yang kompleks, mengidentifikasi tren yang signifikan, dan membuat interpretasi yang akurat.
Pengantar Analisis Multivariat

Analisis multivariat merupakan cabang statistika yang digunakan untuk menganalisis data yang terdiri dari lebih dari satu variabel. Berbeda dengan analisis univariat yang hanya fokus pada satu variabel, analisis multivariat memungkinkan kita untuk mengkaji hubungan dan pola antar beberapa variabel secara simultan. Hal ini memberikan pemahaman yang lebih komprehensif dan mendalam dibandingkan dengan hanya menganalisis variabel secara terpisah.
Kemampuan untuk menganalisis hubungan antar variabel ini sangat bermanfaat dalam berbagai bidang. Analisis multivariat memberikan wawasan yang berharga untuk pengambilan keputusan yang lebih akurat dan efektif.
Penerapan Analisis Multivariat di Berbagai Bidang
Analisis multivariat memiliki aplikasi yang luas di berbagai disiplin ilmu. Berikut beberapa contoh penerapannya:
- Bisnis dan Pemasaran: Analisis multivariat digunakan untuk memahami preferensi konsumen, memprediksi penjualan, dan mengoptimalkan strategi pemasaran. Misalnya, analisis klaster dapat mengelompokkan konsumen berdasarkan karakteristik demografis dan perilaku pembelian mereka, sehingga perusahaan dapat menargetkan kampanye pemasaran yang lebih efektif.
- Kedokteran dan Kesehatan: Dalam bidang kesehatan, analisis multivariat digunakan untuk mengidentifikasi faktor risiko penyakit, memprediksi respons pasien terhadap pengobatan, dan mengembangkan model diagnostik. Contohnya, analisis regresi dapat digunakan untuk mengidentifikasi faktor-faktor yang berkontribusi terhadap perkembangan penyakit jantung koroner.
- Ilmu Lingkungan: Analisis multivariat dapat digunakan untuk menganalisis data lingkungan yang kompleks, seperti kualitas udara dan air. Contohnya, analisis komponen utama dapat digunakan untuk mereduksi dimensi data dan mengidentifikasi polutan utama yang mempengaruhi kualitas air di suatu wilayah.
Perbandingan Metode Analisis Multivariat
Terdapat berbagai metode analisis multivariat, masing-masing dengan karakteristik dan tujuan yang berbeda. Berikut tabel perbandingan beberapa metode tersebut:
| Metode | Jenis Data | Tujuan Analisis | Contoh Penerapan |
|---|---|---|---|
| Analisis Regresi Linier Berganda | Numerik | Mempelajari hubungan antara satu variabel dependen numerik dan beberapa variabel independen numerik | Memprediksi harga rumah berdasarkan luas tanah, jumlah kamar tidur, dan lokasi |
| Analisis Faktor | Numerik | Mereduksi jumlah variabel menjadi beberapa faktor yang lebih sedikit namun masih menjelaskan sebagian besar variansi data | Mengidentifikasi faktor-faktor utama yang mempengaruhi kepuasan pelanggan |
| Analisis Klaster | Numerik dan Kategorik | Mengelompokkan objek atau individu berdasarkan kemiripan karakteristik | Mengelompokkan konsumen berdasarkan perilaku pembelian mereka |
| Analisis Diskriminan | Numerik dan Kategorik | Membangun model untuk mengklasifikasikan objek atau individu ke dalam kelompok yang telah ditentukan | Mengklasifikasikan pasien berdasarkan kemungkinan terkena penyakit jantung |
Analisis Regresi Linier Berganda
Analisis regresi linier berganda merupakan salah satu metode analisis multivariat yang paling umum digunakan. Metode ini digunakan untuk memodelkan hubungan linier antara satu variabel dependen numerik dan dua atau lebih variabel independen numerik. Model regresi linier berganda dapat dituliskan sebagai:
Y = β0 + β 1X 1 + β 2X 2 + … + β pX p + ε
di mana Y adalah variabel dependen, X 1, X 2, …, X p adalah variabel independen, β 0 adalah intersep, β 1, β 2, …, β p adalah koefisien regresi, dan ε adalah error term. Asumsi utama dalam analisis regresi linier berganda meliputi linieritas hubungan antara variabel, independensi error term, homoskedastisitas (variansi error term konstan), dan normalitas error term.
Batasan analisis regresi linier berganda meliputi asumsi-asumsi yang harus dipenuhi, potensi multikolinearitas (korelasi tinggi antar variabel independen), dan kemungkinan adanya outlier yang dapat mempengaruhi hasil analisis.
Keunggulan dan Kelemahan Analisis Multivariat
Analisis multivariat menawarkan beberapa keunggulan, antara lain kemampuan untuk menganalisis hubungan kompleks antar variabel, menghasilkan pemahaman yang lebih komprehensif, dan mendukung pengambilan keputusan yang lebih baik. Namun, analisis multivariat juga memiliki kelemahan, seperti kompleksitas interpretasi hasil, kebutuhan data yang besar, dan asumsi-asumsi yang harus dipenuhi. Interpretasi yang salah dapat terjadi jika asumsi-asumsi yang mendasari metode analisis multivariat tidak terpenuhi.
Metode-Metode Analisis Multivariat
Analisis multivariat merupakan sekumpulan teknik statistik yang digunakan untuk menganalisis data dengan lebih dari satu variabel dependen atau independen. Metode ini sangat berguna dalam memahami hubungan kompleks antar variabel dan mengungkap pola tersembunyi dalam dataset yang besar dan kompleks. Berikut ini akan dibahas beberapa metode analisis multivariat yang umum digunakan, beserta penjelasan dan contoh penerapannya.
Analisis Faktor
Analisis faktor bertujuan untuk mereduksi sejumlah besar variabel menjadi sejumlah faktor yang lebih kecil, namun masih mampu menjelaskan sebagian besar variansi data. Proses ini melibatkan identifikasi pola korelasi antar variabel dan pengelompokan variabel-variabel yang berkorelasi tinggi ke dalam faktor-faktor yang mewakili konsep laten (konsep yang tidak teramati secara langsung). Langkah-langkah perhitungannya melibatkan matriks korelasi, ekstraksi faktor (misalnya, metode principal component analysis), rotasi faktor (misalnya, varimax atau promax), dan interpretasi faktor berdasarkan beban faktor (factor loadings).
Ilustrasi Reduksi Dimensi Data dengan Analisis Faktor:
Bayangkan kita memiliki data mengenai preferensi konsumen terhadap 10 atribut produk (misalnya, harga, kualitas, desain, daya tahan, dll.). Data ini berdimensi tinggi (10 dimensi). Melalui analisis faktor, kita dapat mereduksi 10 atribut tersebut menjadi, misalnya, 3 faktor utama: Faktor 1 (Harga dan Kualitas), Faktor 2 (Desain dan Fitur), dan Faktor 3 (Daya Tahan dan Keandalan). Setiap faktor mewakili gabungan dari beberapa atribut asli, sehingga mengurangi kompleksitas data tanpa kehilangan informasi yang signifikan.
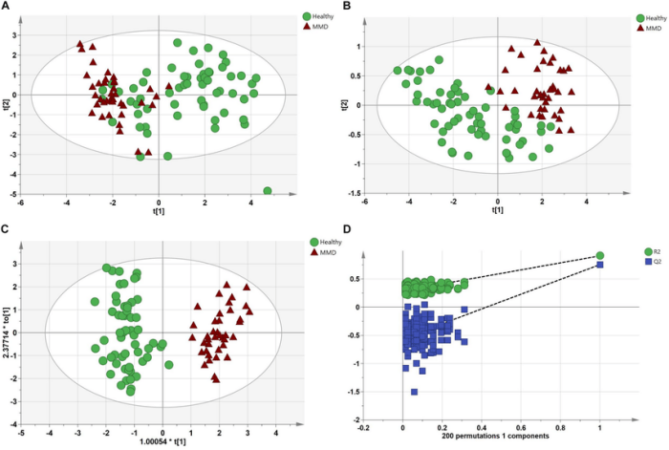
Visualisasinya dapat dibayangkan sebagai proyeksi titik-titik data dari ruang 10 dimensi ke ruang 3 dimensi, di mana setiap dimensi baru mewakili sebuah faktor utama.
Interpretasi dilakukan dengan melihat beban faktor (factor loadings) yang menunjukkan kekuatan hubungan antara setiap variabel dengan setiap faktor. Variabel dengan beban faktor tinggi pada suatu faktor menunjukkan kontribusi yang besar terhadap faktor tersebut.
Analisis Klaster, Analisis multivariat
Analisis klaster bertujuan untuk mengelompokkan objek atau data point ke dalam kelompok (klaster) berdasarkan kesamaan karakteristik mereka. Objek dalam satu klaster memiliki kemiripan yang tinggi satu sama lain, sementara objek dari klaster yang berbeda memiliki perbedaan yang signifikan. Beberapa algoritma yang umum digunakan meliputi:
- K-Means Clustering: Algoritma partisi yang membagi data ke dalam K klaster, dengan K ditentukan sebelumnya.
- Hierarchical Clustering: Algoritma hirarkis yang membangun dendrogram (diagram pohon) untuk menunjukkan hubungan klaster secara bertahap.
- DBSCAN (Density-Based Spatial Clustering of Applications with Noise): Algoritma berbasis kepadatan yang mengidentifikasi klaster sebagai daerah dengan kepadatan titik data yang tinggi.
Analisis Diskriminan
Analisis diskriminan digunakan untuk membedakan dua atau lebih kelompok berdasarkan variabel prediktor. Metode ini membangun fungsi diskriminan yang memaksimalkan perbedaan antar kelompok dan meminimalkan perbedaan di dalam kelompok. Sebagai contoh, analisis diskriminan dapat digunakan untuk membedakan antara pelanggan yang akan melakukan pembelian ulang (kelompok 1) dan pelanggan yang tidak akan melakukan pembelian ulang (kelompok 2) berdasarkan variabel-variabel seperti frekuensi pembelian, nilai transaksi, dan kepuasan pelanggan.
Fungsi diskriminan yang dihasilkan dapat digunakan untuk mengklasifikasikan pelanggan baru ke dalam salah satu kelompok tersebut.
Perbedaan dan Kesamaan Analisis Faktor dan Analisis Komponen Utama
Analisis faktor dan analisis komponen utama (PCA) keduanya merupakan teknik reduksi dimensi, tetapi memiliki perbedaan dalam tujuan dan interpretasi. PCA bertujuan untuk menemukan kombinasi linear dari variabel asli yang menjelaskan variansi maksimum dalam data, tanpa mempertimbangkan struktur laten atau konsep yang mendasarinya. Analisis faktor, di sisi lain, bertujuan untuk mengidentifikasi faktor-faktor laten yang mendasari korelasi antar variabel. Meskipun keduanya menghasilkan komponen atau faktor baru, interpretasi dari komponen atau faktor tersebut berbeda.
Komponen dalam PCA merupakan kombinasi linear dari variabel asli, sedangkan faktor dalam analisis faktor mewakili konsep laten yang tidak teramati secara langsung.
Kesamaan utamanya adalah keduanya berusaha mereduksi dimensi data dan menjelaskan variansi data dengan jumlah variabel yang lebih sedikit. Seringkali, PCA digunakan sebagai langkah awal dalam analisis faktor.
Interpretasi Hasil Analisis Multivariat
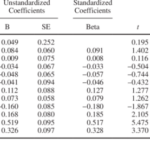
Analisis multivariat, dengan kemampuannya untuk menganalisis sejumlah besar variabel sekaligus, menghasilkan output yang kompleks. Memahami dan menginterpretasikan output ini dengan tepat sangat krusial untuk menarik kesimpulan yang bermakna dan akurat. Bagian ini akan membahas langkah-langkah interpretasi, potensi kesalahan, dan contoh penerapannya dalam studi kasus.
Interpretasi hasil analisis multivariat bergantung pada metode yang digunakan. Namun, beberapa prinsip umum berlaku untuk berbagai teknik, seperti analisis faktor, analisis klaster, dan analisis diskriminan. Pemahaman mendalam tentang metode yang dipilih dan asumsi-asumsinya sangat penting sebelum memulai interpretasi.
Contoh Output dan Interpretasinya
Mari kita perhatikan contoh matriks korelasi sebagai output dari analisis multivariat. Matriks korelasi menunjukkan hubungan linier antara setiap pasangan variabel. Nilai berkisar antara -1 (korelasi negatif sempurna) hingga +1 (korelasi positif sempurna), dengan 0 menunjukkan tidak adanya korelasi linier.
Contoh Matriks Korelasi:
| Variabel | X1 | X2 | X3 |
|—|—|—|—|
| X1 | 1.00 | 0.85 | -0.20 |
| X2 | 0.85 | 1.00 | -0.15 |
| X3 | -0.20 | -0.15 | 1.00 |
Interpretasi: Variabel X1 dan X2 memiliki korelasi positif yang kuat (0.85), sementara X1 dan X3 memiliki korelasi negatif yang lemah (-0.20). Ini menunjukkan bahwa X1 dan X2 cenderung bergerak searah, sedangkan X1 dan X3 cenderung bergerak berlawanan arah.
Interpretasi matriks korelasi ini memberikan gambaran awal tentang hubungan antar variabel. Informasi ini dapat digunakan untuk memilih variabel yang relevan untuk analisis lebih lanjut atau untuk membangun model prediksi.
Panduan Langkah Demi Langkah Interpretasi Output
Berikut adalah panduan langkah demi langkah untuk menginterpretasikan output analisis multivariat, dengan fokus pada pemahaman konteks dan validasi hasil:
- Pahami Tujuan Analisis: Sebelum menginterpretasikan hasil, pastikan Anda memahami tujuan analisis dan pertanyaan penelitian yang ingin dijawab.
- Tinjau Asumsi Metode: Periksa apakah asumsi metode yang digunakan telah terpenuhi. Pelanggaran asumsi dapat memengaruhi validitas hasil.
- Analisis Statistik Deskriptif: Mulailah dengan memeriksa statistik deskriptif dari data, seperti rata-rata, standar deviasi, dan histogram, untuk memahami distribusi data.
- Interpretasi Output Utama: Fokus pada output utama dari analisis, seperti nilai eigen dalam analisis faktor, dendrogram dalam analisis klaster, atau koefisien diskriminan dalam analisis diskriminan.
- Visualisasi Data: Gunakan visualisasi data, seperti scatter plot, grafik batang, atau peta panas, untuk membantu memahami hubungan antar variabel dan hasil analisis.
- Validasi Hasil: Validasi hasil dengan menggunakan metode lain atau dengan membandingkannya dengan pengetahuan sebelumnya.
Potensi Kesalahan Interpretasi dan Cara Mengatasinya
Beberapa kesalahan umum dalam interpretasi analisis multivariat meliputi:
- Korelasi Tidak Sama dengan Kausalitas: Korelasi tinggi antara dua variabel tidak selalu menunjukkan hubungan sebab-akibat.
- Overinterpretasi Hasil: Jangan menarik kesimpulan yang terlalu luas atau spekulatif berdasarkan hasil analisis.
- Mengabaikan Asumsi: Pelanggaran asumsi dapat menyebabkan hasil yang bias atau tidak valid.
- Kurangnya Konteks: Interpretasi hasil harus mempertimbangkan konteks penelitian dan data yang digunakan.
Untuk mengatasi kesalahan-kesalahan ini, penting untuk memahami batasan metode yang digunakan, memeriksa asumsi, dan menggunakan visualisasi data untuk membantu interpretasi.
Contoh Kasus Studi
Sebuah perusahaan ritel ingin memahami faktor-faktor yang memengaruhi kepuasan pelanggan. Mereka menggunakan analisis faktor untuk menganalisis data survei pelanggan yang mencakup berbagai aspek, seperti kualitas produk, layanan pelanggan, dan harga. Hasil analisis faktor mengidentifikasi tiga faktor utama: kualitas produk, kepuasan layanan, dan nilai yang dirasakan. Dengan memahami faktor-faktor ini, perusahaan dapat fokus pada peningkatan aspek-aspek tertentu untuk meningkatkan kepuasan pelanggan.
Visualisasi Data dalam Interpretasi
Visualisasi data memainkan peran penting dalam interpretasi hasil analisis multivariat. Misalnya, dalam analisis klaster, dendrogram dapat menunjukkan bagaimana kelompok-kelompok data terbentuk. Scatter plot dapat digunakan untuk memvisualisasikan hubungan antara dua variabel, sementara peta panas dapat menunjukkan korelasi antar variabel dalam matriks korelasi. Visualisasi ini membantu memahami pola dan tren dalam data yang mungkin tidak terlihat dalam output numerik saja.
Perangkat Lunak dan Aplikasi Analisis Multivariat
Analisis multivariat melibatkan pengolahan data yang kompleks dan membutuhkan perangkat lunak yang tepat untuk menghasilkan hasil yang akurat dan efisien. Pemilihan perangkat lunak yang tepat sangat bergantung pada jenis data, metode analisis yang digunakan, dan kemampuan pengguna. Berikut ini akan dibahas beberapa perangkat lunak populer, fitur-fiturnya, serta panduan pemilihannya.
Perangkat Lunak Analisis Multivariat yang Umum Digunakan
Beberapa perangkat lunak populer yang digunakan untuk analisis multivariat meliputi SPSS, R, SAS, dan Python dengan library seperti scikit-learn. Masing-masing memiliki kelebihan dan kekurangan yang perlu dipertimbangkan.
Perbandingan Fitur dan Keunggulan Perangkat Lunak
| Nama Perangkat Lunak | Fitur Utama | Keunggulan | Kelemahan |
|---|---|---|---|
| SPSS | Analisis faktor, regresi linear berganda, analisis klaster, ANOVA, uji-t | Antarmuka pengguna yang ramah, mudah dipelajari, dokumentasi yang lengkap. | Harga relatif mahal, fleksibilitas terbatas untuk analisis yang lebih kompleks. |
| R | Beragam paket analisis statistik, fleksibilitas tinggi, open-source. | Gratis, fleksibel, komunitas pengguna yang besar dan aktif, banyak paket tambahan. | Kurva belajar yang curam, antarmuka pengguna yang kurang user-friendly dibandingkan SPSS. |
| SAS | Analisis statistik yang komprehensif, kemampuan pemrosesan data besar, visualisasi data yang baik. | Kemampuan pemrosesan data yang sangat baik, cocok untuk data besar dan kompleks. | Harga yang mahal, kurva belajar yang cukup tinggi. |
| Python (dengan scikit-learn) | Algoritma machine learning yang beragam, fleksibilitas tinggi, integrasi dengan bahasa pemrograman lain. | Gratis, fleksibel, cocok untuk integrasi dengan sistem lain, banyak library pendukung. | Membutuhkan pemahaman pemrograman Python, kurva belajar yang cukup tinggi. |
Pemilihan Perangkat Lunak yang Tepat
Pemilihan perangkat lunak bergantung pada beberapa faktor, termasuk jenis data (kuantitatif, kualitatif, campuran), metode analisis yang dibutuhkan (regresi, klasifikasi, pengelompokan), anggaran, dan keahlian pengguna. Untuk data sederhana dan analisis dasar, SPSS mungkin cukup. Untuk analisis yang lebih kompleks dan data besar, R atau SAS mungkin lebih cocok. Python menawarkan fleksibilitas tinggi dan integrasi dengan berbagai sistem, tetapi membutuhkan keahlian pemrograman.
Contoh Skenario Penggunaan Perangkat Lunak Analisis Multivariat
Sebuah perusahaan ritel dapat menggunakan SPSS untuk menganalisis data penjualan dan preferensi pelanggan untuk mengidentifikasi segmen pasar yang berbeda dan mengoptimalkan strategi pemasaran. Sebuah peneliti medis dapat menggunakan R untuk menganalisis data genetik untuk mengidentifikasi faktor risiko penyakit tertentu. Sebuah perusahaan keuangan dapat menggunakan Python untuk membangun model prediksi risiko kredit.
Alur Kerja Analisis Multivariat Menggunakan R
Sebagai contoh, alur kerja analisis multivariat menggunakan R untuk analisis klaster pelanggan dapat diuraikan sebagai berikut: Pertama, data pelanggan (misalnya, demografi, riwayat pembelian) diimpor ke R. Kemudian, data dibersihkan dan dipreparasi (misalnya, penanganan nilai hilang, standarisasi data). Selanjutnya, algoritma klastering (misalnya, k-means) diterapkan. Hasil klastering kemudian divisualisasikan dan diinterpretasi untuk mengidentifikasi karakteristik masing-masing segmen pelanggan. Terakhir, hasil analisis digunakan untuk membuat keputusan bisnis, seperti penargetan pemasaran yang lebih efektif.
Pemungkas
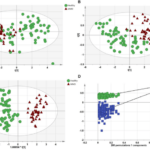
Analisis multivariat menawarkan alat yang sangat berharga untuk menavigasi kompleksitas data di dunia modern. Dengan memahami berbagai metode dan interpretasinya, kita dapat mengungkap wawasan yang berharga dan membuat keputusan yang lebih tepat. Meskipun terdapat potensi kesalahan interpretasi, dengan pendekatan yang hati-hati dan penggunaan perangkat lunak yang tepat, analisis multivariat dapat memberikan pemahaman yang mendalam tentang fenomena yang kompleks dan memberikan kontribusi signifikan dalam berbagai disiplin ilmu.