Akar 15, sebuah bilangan irasional yang menarik perhatian karena posisinya di antara bilangan bulat. Nilai desimalnya, meskipun tak berujung dan tak berpola, memiliki peran penting dalam berbagai bidang, mulai dari geometri sederhana hingga persamaan matematika yang kompleks. Eksplorasi lebih lanjut akan mengungkap keunikan dan aplikasi akar 15 dalam berbagai konteks.
Kita akan menjelajahi perhitungan nilai akar 15, representasi geometrisnya, dan perbandingannya dengan akar bilangan bulat terdekat. Selanjutnya, kita akan melihat bagaimana akar 15 berperan dalam persamaan kuadrat, trigonometri, teorema Pythagoras, serta aplikasinya dalam fisika dan pemodelan matematika. Perjalanan ini akan memberikan pemahaman yang lebih komprehensif tentang bilangan irasional yang satu ini.
Nilai Akar 15
Akar 15, atau √15, merupakan bilangan irasional, artinya ia tidak dapat dinyatakan sebagai pecahan sederhana dari dua bilangan bulat. Nilai desimalnya tidak berulang dan tidak berakhir. Pembahasan berikut akan mengeksplorasi nilai akar 15 dari berbagai perspektif, mulai dari perhitungan numerik hingga representasi geometriknya.
Nilai Desimal Akar 15
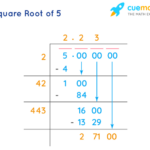
Dengan menggunakan kalkulator atau perangkat lunak matematika, nilai akar 15 hingga empat angka di belakang koma adalah 3.8730. Perlu diingat bahwa ini hanyalah pendekatan, karena nilai sebenarnya memiliki jumlah desimal yang tak terhingga.
Representasi Geometri Akar 15
Akar 15 dapat direpresentasikan secara geometrik sebagai panjang diagonal suatu persegi panjang. Bayangkan sebuah persegi panjang dengan panjang sisi 3 satuan dan lebar 2 satuan. Dengan menggunakan teorema Pythagoras (a² + b² = c²), panjang diagonalnya (c) dapat dihitung: 3² + 2² = 9 + 4 = 13. Panjang diagonalnya adalah √13. Untuk merepresentasikan √15, kita perlu mencari persegi panjang dengan panjang sisi yang menghasilkan 15 ketika dikuadratkan dan dijumlahkan.
Salah satu kemungkinan adalah persegi panjang dengan sisi sepanjang √5 dan √10. Karena √5 ≈ 2.236 dan √10 ≈ 3.162, kita dapat gambarkan persegi panjang dengan sisi-sisi yang mendekati nilai tersebut. Diagonal persegi panjang ini akan merepresentasikan akar 15. Persegi panjang lain juga mungkin, asalkan memenuhi persamaan Pythagoras sehingga sisi-sisinya dikuadratkan dan dijumlahkan menghasilkan 15.
Perbandingan Akar 15 dengan Akar Bilangan Bulat Terdekat
Akar 16 (√16 = 4) dan akar 9 (√9 = 3) merupakan akar kuadrat dari bilangan bulat terdekat dengan
15. Perbedaannya adalah: √15 – √9 = 3.8730 – 3 = 0.8730 dan √16 – √15 = 4 – 3.8730 = 0.1270. Ini menunjukkan bahwa nilai akar 15 lebih dekat ke akar 16 daripada akar 9.
Tabel Perbandingan Akar 15 dengan Akar Bilangan Terdekat
| Bilangan | Akar Kuadrat | Perbedaan dengan akar 15 |
|---|---|---|
| 14 | 3.7417 | 0.1313 |
| 15 | 3.8730 | 0 |
| 16 | 4 | 0.1270 |
| 25 | 5 | 1.1270 |
Algoritma Iteratif untuk Menghitung Akar 15 (Metode Newton-Raphson)
Metode Newton-Raphson adalah metode iteratif yang dapat digunakan untuk mencari akar dari suatu fungsi. Untuk menghitung akar 15, kita dapat menggunakan fungsi f(x) = x²
–
15. Tujuannya adalah menemukan nilai x yang membuat f(x) =
0. Rumus iterasi Newton-Raphson adalah: x n+1 = x n
-f(x n) / f'(x n), dimana f'(x n) adalah turunan pertama dari f(x).
Dalam kasus ini, f'(x) = 2x. Dengan mengambil nilai awal x 0 (misalnya, 4), kita dapat melakukan iterasi berulang hingga mencapai tingkat akurasi yang diinginkan. Setiap iterasi akan menghasilkan nilai x yang semakin mendekati akar 15.
- Pilih nilai awal x0 (misalnya, 4).
- Hitung x n+1 = x n
- (x n²
- 15) / (2x n).
- Ulangi langkah 2 hingga perbedaan antara x n+1 dan x n cukup kecil (mencapai tingkat akurasi yang diinginkan).
Akar 15 dalam Persamaan Matematika

Akar 15, meskipun bukan bilangan bulat atau pecahan sederhana, merupakan bilangan irasional yang sering muncul dalam berbagai konteks matematika. Pemahaman tentang akar 15 penting untuk menyelesaikan berbagai jenis persamaan dan soal aplikasi, terutama dalam geometri dan trigonometri.
Persamaan Kuadrat dengan Akar 15 sebagai Salah Satu Akarnya
Salah satu cara untuk membentuk persamaan kuadrat dengan akar 15 sebagai salah satu akarnya adalah dengan memanfaatkan sifat-sifat akar persamaan kuadrat. Misalnya, jika x = √15 adalah salah satu akar, maka (x – √15) adalah salah satu faktor. Untuk mendapatkan persamaan kuadrat, kita dapat mengalikan faktor ini dengan faktor lain, misalnya (x + √15). Hasil perkaliannya adalah x²
-15 = 0.
Persamaan ini memiliki akar-akar x = √15 dan x = -√15. Langkah penyelesaiannya melibatkan pemfaktoran atau rumus kuadrat.
Penerapan Akar 15 dalam Geometri: Mencari Panjang Diagonal Persegi Panjang
Misalkan kita memiliki sebuah persegi panjang dengan panjang 4 cm dan lebar 3 cm. Untuk mencari panjang diagonalnya, kita dapat menggunakan Teorema Pythagoras. Panjang diagonal (d) dapat dihitung dengan rumus d² = panjang² + lebar². Dalam kasus ini, d² = 4² + 3² = 16 + 9 = 25. Oleh karena itu, d = √25 = 5 cm.
Namun, jika panjang persegi panjang adalah 2 cm dan lebarnya adalah √11 cm, maka panjang diagonalnya adalah √(2² + (√11)²) = √(4 + 11) = √15 cm.
Penggunaan Akar 15 dalam Persamaan Trigonometri
Akar 15 dapat muncul dalam penyelesaian persamaan trigonometri yang melibatkan sudut-sudut khusus atau nilai-nilai fungsi trigonometri tertentu. Misalnya, perhatikan persamaan tan θ = √15. Untuk menyelesaikannya, kita perlu mencari nilai θ yang memenuhi persamaan tersebut. Dengan menggunakan kalkulator atau tabel trigonometri, kita dapat menemukan nilai θ (dalam radian atau derajat).
Penerapan Akar 15 dalam Teorema Pythagoras
Perhatikan segitiga siku-siku ABC dengan sudut siku-siku di C. Jika panjang sisi AB (hipotenusa) adalah √15 cm dan panjang sisi BC adalah 1 cm, maka panjang sisi AC dapat dihitung menggunakan teorema Pythagoras: AC² + BC² = AB². Substitusikan nilai yang diketahui: AC² + 1² = (√15)². Maka AC² = 15 – 1 = 14, sehingga AC = √14 cm.
Jenis Persamaan Matematika yang Melibatkan Akar 15
Akar 15 dapat muncul dalam berbagai jenis persamaan matematika. Berikut beberapa contohnya:
- Persamaan Kuadrat: x²
15 = 0 (seperti yang dijelaskan sebelumnya).
- Persamaan Irasional: √(x + 6) = √15. Penyelesaiannya melibatkan kuadratkan kedua ruas, sehingga x + 6 = 15, dan x = 9.
- Persamaan Trigonometri: sin θ = √15/4. Penyelesaiannya melibatkan mencari nilai sudut θ yang memenuhi persamaan tersebut menggunakan kalkulator atau tabel trigonometri.
Akar 15 dalam Konteks Lain
Angka irrasional seperti akar 15, meskipun tidak tampak sering digunakan dalam kehidupan sehari-hari seperti bilangan bulat, memiliki peran penting dalam berbagai bidang ilmu dan matematika. Pemahaman tentang akar 15 dan sifat-sifatnya memperkaya pemahaman kita tentang sistem bilangan dan aplikasinya dalam memecahkan masalah yang kompleks.
Akar 15 dalam Fisika dan Ilmu Teknik
Akar 15 dapat muncul dalam perhitungan yang melibatkan vektor dan geometri. Misalnya, dalam mekanika, perhitungan resultan gaya pada suatu objek yang membentuk sudut tertentu dapat menghasilkan nilai yang melibatkan akar 15. Bayangkan sebuah balok ditarik oleh dua gaya dengan besar yang berbeda dan membentuk sudut 120 derajat. Perhitungan resultan gaya akan melibatkan operasi matematika yang menghasilkan nilai yang mengandung akar 15.
Penerapan lain dapat ditemukan dalam perhitungan panjang diagonal pada bangun ruang tertentu atau dalam analisis tegangan pada struktur bangunan.
Akar 15 dalam Pemodelan Matematika Fenomena Alam
Dalam pemodelan matematika, akar 15 bisa muncul sebagai solusi dari persamaan diferensial yang menggambarkan fenomena alam. Misalnya, dalam simulasi gelombang air, solusi persamaan gelombang dapat menghasilkan nilai yang mengandung akar 15, tergantung pada kondisi awal dan parameter sistem. Meskipun tidak selalu eksplisit, kehadiran akar 15 menunjukkan kompleksitas dan ketepatan model matematika yang digunakan untuk mendekati realitas.
Akar 15 sebagai Bilangan Irasional
Akar 15 termasuk dalam kategori bilangan irasional, yaitu bilangan yang tidak dapat dinyatakan sebagai pecahan dari dua bilangan bulat. Sifat utama bilangan irasional adalah representasinya yang tak berujung dan tidak berulang jika dinyatakan dalam bentuk desimal. Akar 15 memiliki sifat ini, dan ketidakmampuan untuk menyatakannya sebagai pecahan sederhana mencerminkan kompleksitas dan keunikannya dalam sistem bilangan.
Representasi Visual Akar 15
Akar 15 dapat divisualisasikan sebagai panjang diagonal sebuah persegi panjang dengan sisi 3 dan 5. Bayangkan sebuah persegi panjang dengan panjang sisi 3 satuan dan lebar 5 satuan. Diagonal persegi panjang tersebut akan memiliki panjang yang sama dengan akar kuadrat dari (3² + 5²), yaitu akar 34. Namun, jika kita pertimbangkan sebuah segitiga siku-siku dengan sisi-sisi 2 dan √11, maka hipotenusanya akan bernilai √15.
Hal ini dapat digambarkan sebagai segitiga siku-siku dengan satu sisi sepanjang 2 satuan dan sisi lainnya sepanjang √11 satuan. Hipotenusa segitiga ini, yang dihitung menggunakan teorema Pythagoras, akan mewakili panjang akar 15.
Relevansi Akar 15 dalam Matematika Modern
Dalam matematika modern, akar 15 berperan sebagai contoh konkret dari bilangan irasional dan contributes to a deeper understanding of number systems and their properties. Kehadirannya dalam berbagai konteks matematika, seperti aljabar, kalkulus, dan geometri, menunjukkan peran pentingnya dalam pengembangan dan pemahaman konsep matematika yang lebih luas. Akar 15, meskipun mungkin tampak sederhana, merupakan elemen penting dalam struktur matematika yang lebih kompleks.
Ulasan Penutup: Akar 15
Akar 15, meskipun tampak sederhana, menyimpan kekayaan matematis yang signifikan. Dari perhitungan nilai desimalnya hingga penerapannya dalam berbagai persamaan dan model, akar 15 menunjukkan betapa pentingnya pemahaman mendalam tentang bilangan irasional dalam berbagai disiplin ilmu. Memahami akar 15 tidak hanya memperluas pengetahuan matematika kita, tetapi juga membuka wawasan baru dalam memahami dunia di sekitar kita.