Akar 32, sebuah bilangan irasional yang menarik untuk dikaji. Angka ini mungkin terlihat sederhana, namun menyimpan misteri matematika yang menarik untuk diungkap. Dari bentuk sederhananya hingga penerapannya dalam berbagai perhitungan, akar 32 menawarkan wawasan yang kaya tentang konsep akar kuadrat dan hubungannya dengan bilangan lain.
Kita akan menjelajahi faktorisasi prima dari 32, menghitung perkiraan nilainya, serta melihat bagaimana akar 32 diaplikasikan dalam geometri dan persamaan kuadrat. Selain itu, kita akan menganalisis hubungannya dengan bilangan lain dan melakukan beberapa operasi matematika dasar untuk memahami sifat-sifatnya secara lebih mendalam.
Bentuk Sederhana dan Faktorisasi
Akar kuadrat dari 32, atau √32, bukanlah bilangan bulat. Namun, kita dapat menyederhanakannya ke bentuk yang lebih ringkas dan memahami komposisinya melalui faktorisasi prima. Proses ini akan membantu kita memahami struktur bilangan tersebut dan merepresentasikannya dalam bentuk yang lebih efisien.
Faktorisasi Prima 32
Faktorisasi prima adalah proses memecah suatu bilangan menjadi perkalian bilangan-bilangan prima. Bilangan prima adalah bilangan bulat lebih besar dari 1 yang hanya habis dibagi oleh 1 dan dirinya sendiri. Untuk 32, kita dapat melakukan faktorisasi sebagai berikut:
- 32 dibagi 2 hasilnya 16.
- 16 dibagi 2 hasilnya 8.
- 8 dibagi 2 hasilnya 4.
- 4 dibagi 2 hasilnya 2.
- 2 dibagi 2 hasilnya 1.
Jadi, faktorisasi prima dari 32 adalah 2 x 2 x 2 x 2 x 2 = 2 5.
Akar 32 sebagai Perkalian Akar Bilangan Prima
Dengan mengetahui faktorisasi prima 32, kita dapat menyederhanakan akar
32. Karena 32 = 2 5, maka √32 = √(2 5). Kita dapat memisahkannya menjadi:
√32 = √(24 x 2) = √(2 4) x √2 = 2 2√2 = 4√2
Oleh karena itu, akar 32 dalam bentuk paling sederhana adalah 4√2.
Tabel Faktor dan Akar Kuadrat
Berikut tabel yang menampilkan beberapa faktor dari 32 dan akar kuadratnya:
| Faktor | Akar Kuadrat |
|---|---|
| 1 | 1 |
| 2 | √2 ≈ 1.414 |
| 4 | 2 |
| 8 | √8 = 2√2 ≈ 2.828 |
| 16 | 4 |
| 32 | 4√2 ≈ 5.657 |
Representasi Visual Faktorisasi Prima 32
Bayangkan sebuah persegi panjang dengan luas 32 satuan persegi. Kita dapat membagi persegi panjang ini menjadi beberapa persegi kecil. Karena faktorisasi prima 32 adalah 2 5, kita bisa membayangkannya sebagai 5 baris dengan masing-masing baris terdiri dari 2 x 2 x 2 = 8 persegi kecil. Akar 32 (4√2) merepresentasikan sisi dari persegi panjang yang jika dikalikan dengan dirinya sendiri akan menghasilkan luas 32.
Karena bukan bilangan bulat, sisi tersebut tidak dapat diukur dengan bilangan bulat, melainkan dengan 4 dikali √2. Konsep ini menunjukkan hubungan antara faktorisasi prima dan akar kuadrat suatu bilangan.
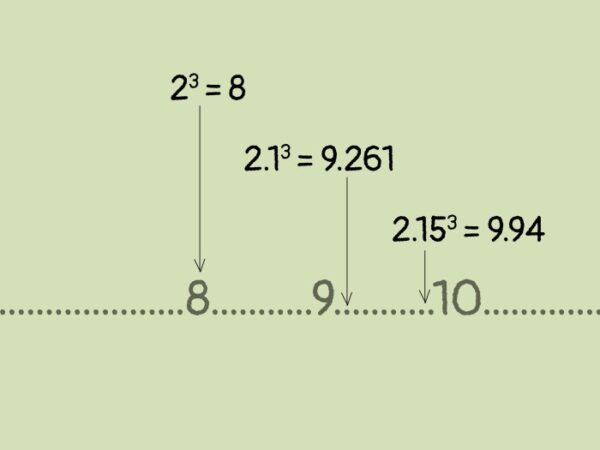
Perkiraan Nilai dan Perbandingan
Setelah memahami konsep akar kuadrat, kita akan menelaah lebih lanjut mengenai perkiraan nilai akar 32 dan membandingkannya dengan akar bilangan bulat terdekat. Hal ini penting untuk membangun pemahaman yang lebih komprehensif tentang bagaimana akar kuadrat bekerja dan bagaimana kita dapat memperkirakan nilainya tanpa menggunakan kalkulator.
Perhitungan akar kuadrat secara manual dapat rumit, terutama untuk bilangan yang tidak merupakan kuadrat sempurna. Oleh karena itu, pendekatan perkiraan menjadi sangat berguna dalam banyak situasi.
Perkiraan Nilai Akar 32
Untuk mendapatkan perkiraan nilai akar 32 dengan dua desimal di belakang koma, kita dapat menggunakan metode iteratif atau memanfaatkan kalkulator. Dengan menggunakan kalkulator, kita temukan bahwa akar 32 kira-kira sama dengan 5.66.
Perbandingan dengan Akar Bilangan Bulat Terdekat
Akar 32 terletak di antara akar 25 (yang sama dengan 5) dan akar 36 (yang sama dengan 6). Ini menunjukkan bahwa nilai akar 32 berada di antara 5 dan 6. Perbedaan antara akar 32 (≈ 5.66) dan akar 25 (5) adalah sekitar 0.66, sementara perbedaan antara akar 32 (≈ 5.66) dan akar 36 (6) adalah sekitar 0.34. Perbedaan ini menunjukkan seberapa dekat perkiraan kita dengan nilai sebenarnya.
Perbedaan Nilai Sebenarnya dan Perkiraan
Perbedaan antara nilai sebenarnya akar 32 dan perkiraan 5.66 bergantung pada tingkat akurasi yang dibutuhkan. Dengan menggunakan kalkulator yang lebih presisi, kita mungkin mendapatkan nilai yang lebih akurat, namun perbedaannya akan tetap sangat kecil dan umumnya dapat diabaikan untuk sebagian besar keperluan praktis. Perbedaan ini biasanya hanya terlihat pada desimal di belakang koma.
Metode Perkiraan yang Digunakan, Akar 32
Metode perkiraan yang digunakan di sini adalah dengan menggunakan kalkulator. Namun, metode numerik seperti metode Newton-Raphson juga dapat digunakan untuk menghitung akar kuadrat dengan tingkat akurasi yang tinggi. Metode ini melibatkan iterasi yang berulang untuk mendekati nilai akar secara bertahap.
Perbandingan dengan Akar Bilangan Lain
Mari kita bandingkan akar 32 dengan akar 16 (yang sama dengan 4) dan akar 64 (yang sama dengan 8). Akar 16 lebih kecil dari akar 32, sedangkan akar 64 lebih besar. Perbedaan antara akar 32 dan akar 16 adalah sekitar 1.66, sedangkan perbedaan antara akar 32 dan akar 64 adalah sekitar 2.34. Perbedaan ini menggambarkan bagaimana jarak akar 32 terhadap bilangan kuadrat sempurna lainnya.
Penerapan dalam Perhitungan: Akar 32
Akar 32, meskipun bukan bilangan bulat, memiliki peran penting dalam berbagai perhitungan, terutama dalam geometri dan penyelesaian persamaan. Kemampuan untuk memanipulasi dan menyederhanakan akar 32 membantu kita menyelesaikan masalah yang tampak kompleks menjadi lebih mudah dipahami dan dihitung.
Penerapan Akar 32 dalam Geometri
Akar 32 sering muncul dalam perhitungan geometri, khususnya ketika kita berurusan dengan diagonal persegi atau segitiga siku-siku. Memahami cara menghitung dan menyederhanakan akar 32 sangat penting untuk mendapatkan hasil yang akurat.
Misalnya, untuk menghitung panjang diagonal sebuah persegi dengan sisi sepanjang 4 satuan, kita dapat menggunakan teorema Pythagoras. Panjang diagonal (d) dapat dihitung dengan rumus:
d = √(4² + 4²) = √(16 + 16) = √32
Akar 32 dapat disederhanakan menjadi 4√2. Oleh karena itu, panjang diagonal persegi tersebut adalah 4√2 satuan.
Akar 32 dalam Penyelesaian Persamaan Kuadrat
Akar 32 juga dapat muncul sebagai solusi dalam persamaan kuadrat. Kemampuan untuk mengenali dan menyederhanakan akar 32 sangat membantu dalam memperoleh akar-akar persamaan tersebut.
Sebagai contoh, perhatikan persamaan kuadrat x²
-32 =
0. Untuk menyelesaikan persamaan ini, kita dapat memindahkan konstanta ke sisi kanan dan kemudian mengambil akar kuadrat dari kedua sisi:
x² = 32
x = ±√32
x = ±4√2
Oleh karena itu, solusi dari persamaan kuadrat tersebut adalah x = 4√2 dan x = -4√2.
Contoh Penerapan Akar 32 dalam Fisika
Berikut adalah contoh penerapan akar 32 dalam konteks fisika, khususnya dalam perhitungan kecepatan.
Sebuah bola dilempar vertikal ke atas dengan kecepatan awal 8 m/s. Berapa lama waktu yang dibutuhkan bola untuk mencapai ketinggian maksimum jika percepatan gravitasi adalah 10 m/s²?
- Kita dapat menggunakan persamaan kinematika: v f = v i + at, di mana v f adalah kecepatan akhir (0 m/s pada titik tertinggi), v i adalah kecepatan awal (8 m/s), a adalah percepatan (-10 m/s² karena gravitasi), dan t adalah waktu.
- Substitusikan nilai-nilai yang diketahui ke dalam persamaan: 0 = 8 – 10t
- Selesaikan untuk t: 10t = 8 => t = 0.8 s
- Sekarang, mari kita hitung ketinggian maksimum (h) yang dicapai bola menggunakan persamaan: h = v it + ½at²
- Substitusikan nilai-nilai yang diketahui: h = 8(0.8) + ½(-10)(0.8)² = 6.4 – 3.2 = 3.2 m
- Selanjutnya, jika kita ingin menghitung kecepatan bola saat mencapai ketinggian 1.6 meter, kita dapat menggunakan persamaan: v f² = v i² + 2ah
- Substitusikan nilai-nilai yang diketahui: v f² = 8² + 2(-10)(1.6) = 64 – 32 = 32
- Akar kuadrat dari 32 memberikan kecepatan bola pada ketinggian 1.6 meter: v f = √32 = 4√2 m/s
Hubungan dengan Bilangan Lain

Akar 32, atau √32, memiliki hubungan yang menarik dengan bilangan lain, terutama dalam konteks pangkat dua dan klasifikasi bilangan rasional dan irasional. Pemahaman tentang hubungan ini memperkaya pemahaman kita tentang sifat-sifat bilangan dan operasi matematika yang melibatkan akar kuadrat.
Hubungan Akar 32 dengan Pangkat Dua
Akar 32 dapat diartikan sebagai bilangan yang jika dikuadratkan (dipangkatkan dua) akan menghasilkan
32. Dengan kata lain, √32 adalah solusi dari persamaan x² =
32. Meskipun tidak merupakan bilangan bulat, √32 dapat disederhanakan menjadi bentuk 4√
2. Ini berarti bahwa 4√2 jika dikuadratkan menghasilkan 32: (4√2)² = 16
– 2 = 32.
Identifikasi Bilangan yang Dipangkatkan Dua Menghasilkan 32
Tidak ada bilangan bulat yang jika dipangkatkan dua menghasilkan 32. Namun, seperti yang telah dijelaskan, 4√2 adalah bilangan yang memenuhi persyaratan tersebut. Bilangan ini merupakan bilangan irasional, karena tidak dapat dinyatakan sebagai pecahan dari dua bilangan bulat.
Akar 32, Bilangan Rasional dan Irasional
Akar 32 (√32 atau 4√2) adalah contoh bilangan irasional. Bilangan irasional adalah bilangan yang tidak dapat dinyatakan sebagai pecahan dari dua bilangan bulat. Ini berbeda dengan bilangan rasional, yang dapat dinyatakan sebagai pecahan a/b, di mana a dan b adalah bilangan bulat dan b ≠ 0. Sifat irasional dari √32 menunjukkan bahwa representasi desimalnya tidak akan pernah berakhir atau berulang.
Contoh Operasi Matematika Melibatkan Akar 32
Berikut beberapa contoh operasi matematika sederhana yang melibatkan √32 dan bilangan lain:
| Operasi | Bilangan | Hasil | Penjelasan |
|---|---|---|---|
| Penjumlahan | √32 + 5 | ≈ 10.6569 | Menjumlahkan akar 32 dengan 5. Hasilnya adalah bilangan irasional. |
| Pengurangan | √32 – 3 | ≈ 2.6569 | Mengurangi 3 dari akar 32. Hasilnya juga merupakan bilangan irasional. |
| Perkalian | √32 – 2 | 8√2 ≈ 11.3137 | Mengalikan akar 32 dengan 2. Hasilnya masih berupa bilangan irasional. |
| Pembagian | √32 / 4 | √2 ≈ 1.4142 | Membagi akar 32 dengan 4. Hasilnya adalah akar 2, yang juga merupakan bilangan irasional. |
Kesimpulan
Setelah menelusuri berbagai aspek akar 32, dari bentuk paling sederhana hingga penerapannya dalam perhitungan, kita dapat menyimpulkan bahwa pemahaman mendalam tentang akar kuadrat ini sangat penting. Kemampuan untuk mengolah dan memanipulasi akar 32, baik secara teoritis maupun praktis, membuka pintu bagi pemahaman yang lebih luas tentang konsep matematika yang lebih kompleks.